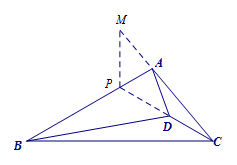
如图，\(D\)为\(\triangle ABC\)内一点，满足\(\angle ABC=\angle BCD=30^\circ\)，\(\angle ABD=\angle ACD\)，\(BD=7\sqrt 3\)，\(AC=5\sqrt 3\)，求\(AD\)的长．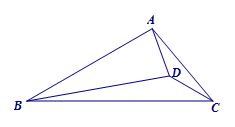
分析 由已知中\(\angle ABC=\angle BCD=30^\circ\)，易得等腰三角形\(PBC\)，再由\(\angle ABD=\angle ACD\)，从而想到去证三角形全等．
方法一 延长\(CD\)与\(AB\)交于点\(P\)，则\[PB=PC,\angle APC=60^\circ.\]又\(\angle ABD=\angle ACD\)，故构造全等，截取\(BQ=AC\)，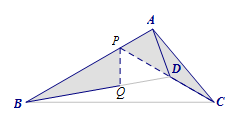
得\[\triangle PBQ\cong \triangle PCA.\]所以\[PQ=PA,\angle BPQ=\angle CPA=60^\circ.\]
从而\[\triangle PDQ\cong \triangle PDA.\]所以\[AD=DQ=BD-AC=2\sqrt 3.\]
方法二 如下图，同法可先证\(\triangle PDB\cong \triangle PMC\)，再证\(\triangle PMA\cong \triangle PDA\)，从而使问题得到解决．