练习题[12] 创新能力培养基础练习

1、对于任意两个实数\(a,b\)，定义运算“\(*\)”如下：\[a*b=\begin{cases}a,a\leqslant b,\\b,a>b.\end{cases}\]那么函数\[f(x)=x^2*\left[(6-x)*(2x+15)\right]\]的最大值为_______．

2、已知\(x,y>0\)，且\(x+y=12\)，则\(\sqrt{x^2+1}+\sqrt{y^2+16}\)的最小值为_______．

3、已知向量序列：\(\overrightarrow{a_1},\overrightarrow{a_2},\cdots,\overrightarrow{a_n},\cdots\)满足如下条件：\(\left|\overrightarrow{a_1}\right|=4\left|\overrightarrow{d}\right|=2\)，\(2\overrightarrow{a_1}\cdot\overrightarrow{d}=-1\)且\(\overrightarrow{a_n}-\overrightarrow{a_{n-1}}=\overrightarrow{d}\)（\(n=2,3,4,\cdots\)）．若\(\overrightarrow{a_1}\cdot\overrightarrow{a_k}=0\)，则\(k=\)_______；\(\left|\overrightarrow{a_i}\right|\)（\(i=1,2,3,\cdots\)）中最小项对应的\(i=\)_______．

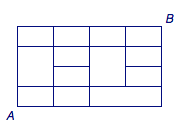
4、如图，从\(A\)到\(B\)，每次只能向右或者向上移动一步，有_______种不同的走法．

 5、已知实数\(a>0\)，\(f(x)=\begin{cases}x^2-2ax,&x\leqslant 1,\\{\log_{\frac 12}}x,&x>1.\end{cases}\)若方程\(f(x)=-\dfrac 34a^2\)有且仅有两个不等实根，且较大实根大于\(2\)，则实数\(a\)的取值范围是_______．

 参考答案

1、\(9\)      提示：利用图象

2、\(13\)      提示：利用勾股定理构造直角三角形

3、\(9\)；\(3\)       提示：利用图形

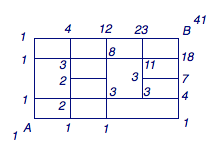
4、\(41\)      提示：如图，每个交叉点处的数等于它左边和下边的数之和

5、\(\left(\dfrac{2\sqrt 3}3,2\right]\)．