每日一题[309] 殊途同归

2010年北京市海淀区高三期末理科数学第8题（选择压轴题）：

点$P$在曲线$C$：$\dfrac{x^2}{4}+y^2=1$上，若存在过$P$的直线交曲线$C$于$A$点，交直线$l$：$x=4$于$B$点，满足$\left|PA\right |=\left|AB\right |$或$\left|PA\right |=\left|PB\right |$，则称点$P$为“$D$点”，那么下列结论正确的是（　    ）

A．曲线$C$上的所有点都是“$D$点”

B．曲线$C$上仅有有限个点是“$D$点”

C．曲线$C$上的所有点都不是“$D$点”

D．曲线$C$上有无穷多个点（但不是所有点）是“$D$点”

正确答案是 D．

解　在这个问题中，$P,A,B$都是动点，其中$P,A$在椭圆上运动，$B$在直线上运动，为了便于思考，我们先固定一个点，看看其它两个点的变化情况，这有些类似于多参数问题中先固定一个参数．

思路一（由意琦行提供）　先固定点$A$，考虑当点$B$在直线上运动时，$P$点形成的轨迹（先不管“点$P$在椭圆上”这个条件），再让点$A$在椭圆上运动起来，考虑所有满足条件的点$P$形成的轨迹，看看这个轨迹与椭圆的关系． 记点集 $$I_1=\left\{P|A\in C,B\in l,\left|PA\right |=\left|PB\right |\right\},$$ 点集 $$I_2=\left\{P|A\in C,B\in l,\left|PA\right |=\left|AB\right |\right\}.$$ 对于点集$I_1$，固定点$A$，让点$B$在直线$l$上运动时，满足条件的$P$形成的集合即直线$l$关于点$A$缩放$\dfrac 12$的直线$l'$．因此，当点$A$在椭圆上移动时，直线$l'$也会随之平行移动，如下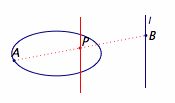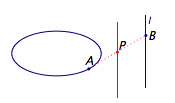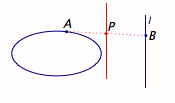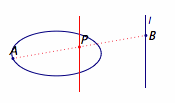： $l'$扫过的区域是如图的带状区域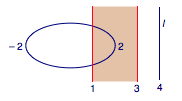： 对于点集$I_2$，当固定点$A$，让$B$在直线上运动时，$P$点形成的轨迹即直线$l$关于点$A$对称的直线$l'$．因此，当点$A$在椭圆上运动时，$l'$扫过的区域为如下的带状区域： 接下来考虑$U=\{P|P\in C\}$与$I_1\cup I_2$的关系，显然，椭圆上有无穷多个“$D$点”，但不是所有点都是“$D$点”，椭圆上不在两个带状区域内的点不是“$D$点”，即横坐标在$(0,1)$之间的椭圆上的点不是“$D$点”．

思路二    在椭圆上任取一点$P(x_0,y_0)$，我们直接考查能否找到满足条件的$A,B$点． 因为$P,A,B$三点共线，所以只需要考虑横坐标即可． 若存在$A,B$满足$\left|PA\right |=\left|PB\right |$，当点$A$从$P$开始运动时，一开始有$|PA|<|PB|$，当点$A$为椭圆的左顶点时，若有$|PA|\geqslant |PB|$，则$A,B$存在，即 $$x_0-(-2)\geqslant 4-x_0,$$ 解得$x_0\geqslant 1.$ 同理，若存在$A,B$满足$\left|PA\right |=\left|AB\right |$，当点$A$从$P$开始运动时，一开始有$|PA|<|AB|$，当点$A$为椭圆的右顶点时，若有$|PA|\geqslant |AB|$，则$A,B$存在，即 $$2-x_0\geqslant 4-2,$$ 解得$x_0\leqslant 0.$ 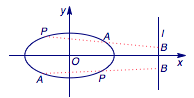综上知，当$x_0\leqslant 0\lor x_0\geqslant 1$时，$P$点为“$D$点”．

思路三　本题也可以纯从代数角度考虑，根据横坐标的关系得到“$D$点”的横坐标范围． 设$P(x_0,y_0)$，因为$P,A,B$三点共线，所以条件$\left|PA\right |=\left|PB\right |$，当且仅当 $$x_A=2x_0-4,$$ 而$x_A\in[-2,2]$，解得 $$x_0\in [1,3].$$ 同理条件$\left|PA\right |=\left|AB\right |$，当且仅当 $$x_A=\dfrac {x_0+4}{2},$$ 由$x_A\in[-2,2]$，解得 $$x_0\in [-8,0].$$ 综上知，当$x_0\in[-2,0]\cup [1,2]$时，$P$点为“$D$点”． 本题的三个思路各有千秋，思路一与椭圆的形状无关，抓住了题目本质；思路二是动点存在性问题的常见思考方向，考虑变化中的边界；思路三在这个题目中最简洁，但可推广性差．不管是哪种方法，都没有直接考虑动直线的问题，而是通过将距离相等转化成了三个点的横坐标的关系，去考虑对这三个点的转化与处理．

下面给出一道练习： 点$P$在直线$l$：$y=x-1$上，若存在过$P$的直线交抛物线$y=x^2$于$A,B$两点，且$|PA|=|AB|$，则称点$P$为“$A$点”，那么下列结论中正确的是(　)

A．直线$l$上的所有点都是“$A$点”

B．直线$l$上仅有有限个点是“$A$点”

C．直线$l$上的所有点都不是“$A$点”

D．直线$l$上有无穷多点（但不是所有点）是“$A$点”

答案　A．

提示　以上三个思路都可以用在本题中，其中第一个思路中$P$形成的轨迹为抛物线的外部，示意图如下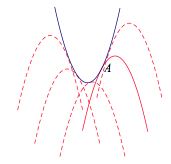： 注　本题为2009年高考北京卷理科数学第8题（选择压轴题）．