每日一题[281] 零点分段讨论与分析端点

2015年高考山东卷理科数学第21题（压轴题）：

设函数$f(x)=\ln (x+1)+a\left( x^2-x\right)$，其中$a\in\mathcal R$．

（1）讨论函数$f(x)$极值点的个数，并说明理由；

（2）若$\forall x>0,f(x)\geqslant 0$成立，求$a$的取值范围．

---

（1）解    根据题意，$f(x)$的导函数

$$f'(x)=\dfrac 1{x+1}\cdot\left( 2ax^2+ax-a+1\right) ,$$ 记其中决定$f'(x)$符号的部分为 $$h(x)=2ax^2+ax-a+1.$$

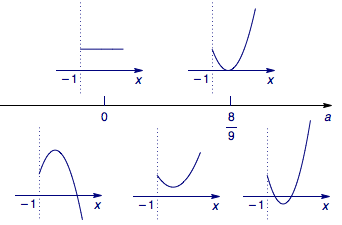
考虑到二次项系数为$2a$，于是$a=0$是一个讨论点；而对称轴为$x=-\dfrac 14$，因此需要考虑判别式

$$\Delta=a^2-4\cdot 2a\cdot (-a+1)=a(9a-8),$$ 因此$a=\dfrac 89$也是一个讨论点．于是可以根据这些讨论点确定讨论轴：

于是不难得到：

当$a<0$时，函数$f(x)$极值点个数为$1$，为极大值点；

当$0\leqslant a \leqslant \dfrac 89$时，函数$f(x)$极值点个数为$0$；

当$a>\dfrac 89$时，函数的极值点个数为$2$，其中有一个极大值点和一个极小值点．

（2）解    注意到区间端点为$0$和$+\infty$．

先分析函数值，由于$f(0+)=0$，而$f(+\infty)$的符号由$a$决定，于是得到必要条件

$$a\geqslant 0,$$ 否则 $$f(x)\leqslant ax^2+(1-a)x,$$ 而当$x>\dfrac{a-1}a$时，$f(x)<0$，矛盾．

在此条件下分析导函数值，由于$h(0+)=-a+1$，$h(+\infty)>0$，于是得到

$$0\leqslant a\leqslant 1,$$ 否则由于$h(1)=2a+1>0$，于是必然存在$m\in (0,1)$，使得$h(m)=0$，且在$[0,m]$上，$h(x)\leqslant 0$，此时易得$f(m)<0$，矛盾．

接下来，结合（1）中对函数$h(x)$的分析可得，当$0\leqslant a\leqslant 1$时，函数$h(x)$满足

$$\forall x>0,h(x)\geqslant 0,$$ 于是函数$f(x)$在$(0,+\infty)$上单调递增，进而结合$f(0)=0$有 $$\forall x>0, f(x)\geqslant 0$$ 成立．

综上，$a$的取值范围是$[0,1]$．