【初级】
已知\(x,y\)为实数，求代数式\(\sqrt{x^2+4}+\sqrt{(6-x)^2+9}\)的最小值．
解 此题如果用代数思想解决会比较麻烦，借助图形就很好解决了．
原式我们可以变形为\[\sqrt {(x-0)^2+(0-2)^2}+\sqrt {(x-6)^2+(0-3)^2}.\]而这种形式恰好就是两点间距离公式．
（注 设\(A(x_1,y_1),B(x_2,y_2)\)，则\(AB=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)．）
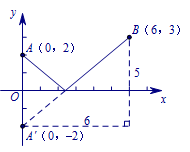如图，原式的最小值就是点\((x,0)\)到点\(A(0,2)\)、点\(B(6,3)\)的距离之和的最小值（利用轴对称作图）．
所以求得原式的最小值为\(\sqrt {61}\)．
【升级】
已知\(x,y\)为实数，求代数式\(\sqrt{1+(y-2)^2}+\sqrt{9+(3-x)^2}+\sqrt{x^2+y^2}\)的最小值．
解 原式可变为\[\sqrt{(0-1)^2+(y-2)^2}+\sqrt{(x-3)^2+(0-3)^2}+\sqrt{(x-0)^2+(0-y)^2}.\]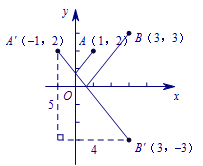
如图，原式的最小值就是点\((0,y)\)到点\(A(1,2)\)、点\((x,0)\)到点\(B(3,3)\)、点\((0,y)\)到点\((x,0)\)的距离之和的最小值（利用轴对称作图）．
所以求得原式的最小值为\(\sqrt{41}\)．