位似旋转变换 设\(O\)为平面上一定点,\(k\)为常数(\(k>0\)),\(\theta\)为有向角,对于任意一点\(P\),射线\(OP\)绕\(O\)旋转角\(\theta\),\(P\)映射到\(P'\),在\(OP'\)射线上存在一点\(P''\),使\(OP'^\prime =kOP'\),把由点\(P\)到点\(P'\prime\)的变换叫做以\(O\)为位似旋转中心、旋转角为\(\theta\)、位似比为\(k\)的位似旋转变换,记为\(S\left(O,\theta,k\right)\).
从位似旋转变换的定义可知,一个位似旋转变换实际是位似变换与旋转变换的复合,此时位似中心与旋转中心重合.位似旋转变换是解决含有特殊系数的线段长度之和的几何极值问题的一种很有效的工具.
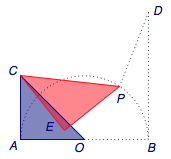
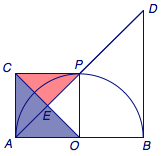
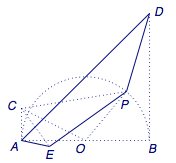
例题 如图,半圆的半径为\(1\),\(AB\)为直径,\(AC\)、\(BD\)为切线,\(AC=1\),\(BD=2\),\(P\)为弧\(AB\)上一动点,求\(\dfrac {\sqrt 2}2PC+PD\)的最小值.
解 注意到\(OC:OA=\sqrt 2:1\),于是可以考虑利用以\(C\)为中心的位似变换,使得\(O\to P\).
如图,设在该位似变换下\(A\to E\),则有\[\dfrac{CP}{EP}=\dfrac{CO}{AO}=\sqrt 2,\]因此\(PE=\dfrac{\sqrt 2}2PC\).
由于该变换下\(A\to E\)且\(O\to P\),于是\[AE=\dfrac{\sqrt 2}2 OP=\dfrac{\sqrt 2}2\]为定值,如上图.
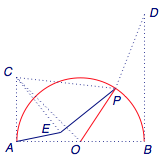
连接\(AD\),有\[AE+EP+PD\geqslant AD,\]可得\[\begin{eqnarray}PE+PD\geqslant AD-AE=\dfrac{3\sqrt 2}2,\end{eqnarray}\]等号当\(A\)、\(E\)、\(P\)、\(D\)四点共线时取得.
如图,当\(P\)位于\(AD\)与半圆的交点处时\(E\)也在线段\(AD\)上,因此不等式(1)中的等号可以取得,因此所求最小值为\(\dfrac{3\sqrt 2}2\).
注 理解了位似旋转变换在解决本题时发挥的作用后,可以尝试将例题推广到更一般的情形,如取\(AC=\dfrac 12\).
此时可以类似的得到\[PE=\dfrac{1}{\sqrt 5}PC,\]且\(AE=\dfrac{1}{\sqrt 5}\)为定值,但是由于\(A\)、\(E\)、\(P\)、\(D\)无法四点共线,可见例题在最后一步具有特殊性,无法推广.