梅氏定理（梅涅劳斯定理）：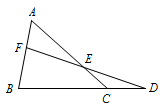 
当直线交\(\triangle ABC\)三边所在直线\(BC,AC,AB\)于点\(D,E ,F\)时，有\(\dfrac {AF}{FB}\cdot \dfrac {BD}{DC}\cdot \dfrac {CE}{EA}=1\)． 塞瓦定理： 
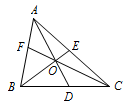在\(\triangle ABC\)内任取一点\(O\)，延长\(AO,BO,CO\)分别交对边于\(D,E,F\)，则\(\dfrac {BD}{DC}\cdot \dfrac {CE}{EA}\cdot \dfrac {AF}{FB}=1\)．
本题要通过梅氏定理与赛瓦定理来解决： \(\triangle ABC\)内有一点\(P\)，连结\(AP,BP,CP\)并延长，分别与对边相交，把\(\triangle ABC\)分成六个小三角形，若这六个小三角形中有三个面积相等，则点\(P\)必为\(\triangle ABC\)的重心．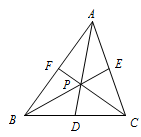 
证明 六个小三角形中有三个面积相等，由对称性可分为四种情况讨论： 情况一 如图①，\(S_{\triangle PBF}=S_{\triangle DPB}=S_ {\triangle PDC}\)； 
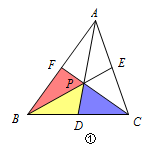此时\(BD=CD\)，所以\(\dfrac{CP}{PF}=2\)， 由梅氏定理可得\(\dfrac{CP}{PF}\cdot \dfrac{AF}{AB}\cdot\dfrac{BD}{DC}=1\)， 所以\(AF=BF\)，即\(P\)为重心． 情况二 如图②，\(S_{\triangle APF}=S_{\triangle DPB}=S_ {\triangle PDC}\)； 
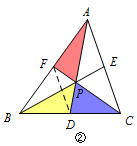可得\(S_{\triangle AFC}=S_{\triangle ADC}\)， 所以\(DF\parallel AC\)， 所以\(D,F\)分别为\(BC,AB\)中点，即\(P\)为重心． 情况三 如图③，\(S_{\triangle FBP}=S_{\triangle DPB}=S_ {\triangle AEP}\)； 
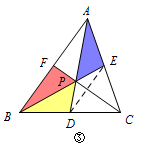此时有\(DE\parallel AB\)， 根据塞瓦定理得\(\dfrac{AF}{BF}\cdot \dfrac{BD}{DC}\cdot \dfrac{CE}{AE}=1\)， 所以\(AF=BF\)，于是\(S_{\triangle APF}=S_{\triangle BPF}\)， 由情况①可得\(P\)为重心． 情况四 如图④，\(S_{\triangle AFP}=S_{\triangle DPB}=S_ {\triangle PCE}\)； 
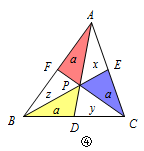根据塞瓦定理得\(\dfrac{S_{\triangle BDP}}{S_{\triangle PDC}}\cdot \dfrac{S_{\triangle PCE}}{S_{\triangle APE}}\cdot \dfrac{S_{\triangle AFP}}{S_{\triangle BFP}}=1\)， 设相等的三角形面积为\(a\)，\(\triangle APE,\triangle CDP\)与\(\triangle BFP\)的面积分别为\(x,y\)与\(z\)，所以\(xyz=a^3\)． ① 若\(x,y,z\)互不相等，不妨设\(x>y>z\)，则\(x>a\)，\(z<a\)，但\[1<\dfrac xa=\dfrac{AE}{CE}=\dfrac{S_{\triangle AEP}}{S_{\triangle CEP}}=\dfrac{S_{\triangle ABP}}{S_{\triangle BCP}}=\dfrac{a+z}{a+y}<1，\]结论矛盾； ② 若\(x,y,z\)中有相等，不妨设\(x=y\)，则\(\dfrac az=\dfrac {a+x}{a+y}=1\)，所以\(a=z\)， 由\(xyz=a^3\)得\(xy=a^2\)，所以\(x=y=z=a\)， 即点\(D,E,F\)分别为各边的中点，\(P\)为重心． 综上，点\(P\)必为\(\triangle ABC\)的重心．