一 到定点的距离相等形成的圆弧
题1 如图，直角梯形\(ABCD\)中，\(\angle BAD=\angle ADC=90^\circ\)，\(AD=CD=\dfrac 12AB=4\)，点\(P\)是线段\(AD\)上的一动点，将\(\triangle ABP\)沿\(BP\)翻折到\(\triangle A'BP\)，连接\(A'C\)，\(A'D\)． （1）当点\(P\)在\(AD\)上运动时，求\(A'C\)的最小值； （2）当点\(P\)在\(AD\)上运动时，求\(A'D\)的最小值； （3）当点\(P\)在\(AD\)上运动时，求\(A'C+A'D\)的最小值．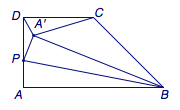 
正确答案是（1）\(8-4\sqrt 2\)；（2）\(4\sqrt 5-8\)；（3）\(4\)． 
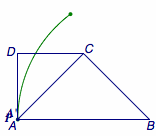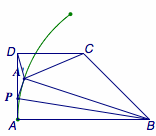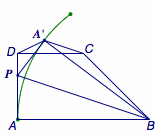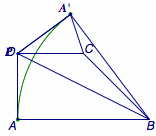点\(A'\)的轨迹为以\(B\)为圆心，\(BA\)为半径的圆弧．
二 对定线段所张角为定角形成的圆弧（一）
题2 如图，以\(G(0,1)\)为圆心，半径为\(2\)的圆与\(x\)轴交于\(A\)、\(B\)两点，与\(y\)轴交于\(C\)、\(D\)两点，点\(E\)为\(\odot G\)上一动点，\(CF\perp AE\)于\(F\)，当点\(E\)从点\(B\)出发顺时针运动到点\(D\)时，点\(F\)所经过的路径长为 ．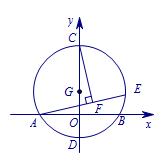 
正确答案是 \(\dfrac {\sqrt 3}3\pi\)． 
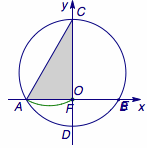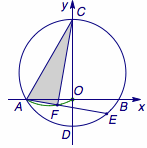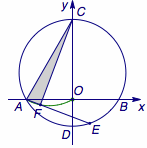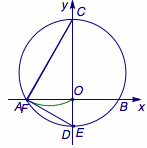点\(F\)的轨迹为以\(AC\)为直径的弧\(OA\)，长度为\(\dfrac {\sqrt 3}3\pi\)．
题3 如图，\(E\)、\(F\)是正方形\(ABCD\)的边\(AD\)上的两个动点，满足\(AE=DF\)，连接\(CF\)交\(BD\)于\(G\)，连接\(BE\)交\(AG\)于点\(H\)，若正方形的边长为\(2\)，则点\(H\)的运动路径长为_______，线段\(DH\)长度的最小值为_______．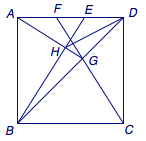 
答案是\(\dfrac {\pi}2\)，\(\sqrt 5-1\)．
点\(H\)的轨迹是以\(AB\)为直径的弧．
三 对定线段所张角为定角形成的圆弧（二）
题4 如图，弓形\(BAC\)中，\(\angle BAC=60^\circ\)，\(BC=2\sqrt 3\)，\(I\)为\(\triangle ABC\)内一点，且满足\(\angle BIC=120^\circ\)，当点\(P\)在优弧\(BAC\)上由点\(B\)向点\(C\)移动，则\(I\)的运动路径长为_______．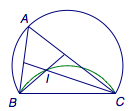 
答案是\(\dfrac 43\pi\)． 
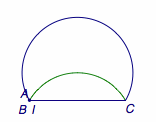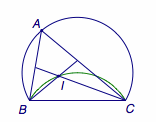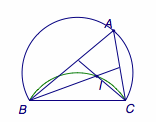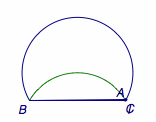点\(I\)的轨迹是以\(BC\)为弦的圆弧，可以参考“等张角线”．
注 此题可以改编为 等边\(\triangle ABC\)边长为\(2\)，射线\(AM\parallel BC\)，\(P\)是射线\(AM\)上一动点（不与\(A\)重合），\(\triangle APC\)的外接圆交\(BP\)于点\(Q\)，则\(AQ\)长的最小值为_______．（\(\dfrac{2\sqrt 3}3\)）
四 旋转位似形成的线段
题5 如图，在边长为\(3\)的等边\(\triangle ABC\)中，\(P\)为\(AC\)边上一动点，\(Q\)为线段\(PC\)上一点，\(\angle PBQ=30^\circ\)，\(D\)为\(BQ\)延长线上一点，\(PD=PB\)，当点\(P\)从点\(A\)运动到\(AP=\dfrac 12AC\)时，点\(D\)经过的路径长度为_______．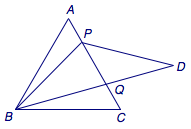 
答案是\(\dfrac {3\sqrt 3}2\)． 
点\(D\)所经过的路径为线段\(MN\)，长度为\(\dfrac {3\sqrt 3}2\)．