如图，已知\(\triangle ABC\)中，\(\angle BAC=45^\circ\)，\(AD\perp BC\)于点\(D\)，若\(BD=2\)，\(CD=1\)，求\(\triangle ABC\)的面积．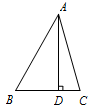
分析 观察图形，发现是角含半角模型图的一部分（如下图），那么是否可以用该模型来解决本题呢？
证明 （方法一）作\(\triangle DAB\)关于\(AB\)对称的\(\triangle EAB\)，作\(\triangle DAC\)关于\(AC\)对称的\(\triangle FAC\)，延长\(FC\)，\(EB\)交于点\(G\)．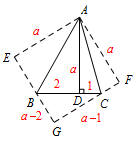
由已知可得四边形\(AEGF\)是正方形，\(EB=2\)，\(FC=1\)，
设正方形边长为\(a\)，则\(AD=a\)，所以\(BG=a-2\)，\(GC=a-1\)．
在\({\rm Rt}\triangle BCG\)中，\[(a-2)^2+(a-1)^2=3^2,\]解得\[a=\dfrac{3+\sqrt{17}}{2}(负值舍去),\]所以\[S_{\triangle ABC}=\dfrac{9+3\sqrt {17}}{4}.\]
（方法二）将\(\triangle ABD\)绕着点\(A\)逆时针旋转\(90^\circ\)得到\(\triangle AGF\)，
连接\(GC\)，延长\(FG\)，\(DC\)交于点\(E\)，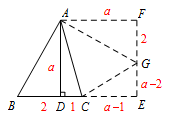
所以四边形\(ADEF\)为正方形，\(\triangle ABC\cong\triangle AGC\)，
设边长为\(a\)，则\(EC=a-1\)，\(EG=a-2\)，
在\({\rm Rt}\triangle ECG\)中，\[(a-2)^2+(a-1)^2=3^2,\]解得\[a=\dfrac{3+\sqrt{17}}{2}(负值舍去),\]所以\[S_{\triangle ABC}=\dfrac{9+3\sqrt {17}}{4}.\]
此题的方法有很多种，从不同角度出发就有不同的解决方法．