每日一题[279] 运动中的规律探索

2013年全国高考数学新课标II卷理科第12题（选择压轴题）：

已知点\(A(-1,0)\)，\(B(1,0)\)，\(C(0,1)\)，直线\(y=ax+b\)（$a>0$）将\(\triangle ABC\)分割为面积相等的两部分，则\(b\)的取值范围是(   )

A．\((0,1)\)

B．\(\left(1-\dfrac{\sqrt 2}{2},\dfrac 12\right)\)

C．\(\left(1-\dfrac{\sqrt 2}{2},\dfrac 13\right]\)

D．\(\left[\dfrac 13,\dfrac 12\right)\)

本题的正确答案是 B．

解　  动直线\(y=ax+b\)的斜率为\(a\)，纵截距为\(b\)，且显然有\(b>0\)．

注意到\(a>0\)，考虑\(a\)的两个边界的情形：

当\(a=0\)时，可以通过直接计算面积得到\[b=1-\dfrac{\sqrt 2}{2}.\] 当\(b<1-\dfrac{\sqrt 2}{2}\)时，结合图象易得右下方的面积始终比左上方的面积小．当\(b>1-\dfrac{\sqrt 2}{2}\)时，\(a\)从\(0\)开始变化，（右）下方的面积开始时比（左）上方面积大，之后(右)下方面积开始减少，如果存在某个时候右下方的面积比左上方的面积小，因为面积连续变化，就能保证存在某个时刻两部分的面积相等．

我们去探索何时右下方的面积比左上方的面积小，此时考虑另一个边界\(a\rightarrow+\infty\)的情形，如图：

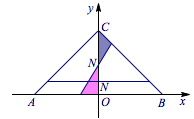右下方的面积大小取决于如图两块阴影面积的大小比较，可以怀疑当\(b=\dfrac 12\)时，这两块面积接近相等．于是我们来分析\(b=\dfrac 12\)的情形：

当\(b\geqslant \dfrac 12\)时，右下方的面积始终比左上方的面积大（\(y\)轴左边的阴影三角形面积始终比右边的阴影三角形的面积大）．

而当\(b<\dfrac 12\)时，当\(a\rightarrow+\infty\)时，必然存在某个时候，右下方的面积比左上方的面积小．所以\[1-\dfrac{\sqrt 2}{2}<b<\dfrac 12\]为所求的范围．

本题也可以从另外一个角度出发：

先探究将\(\triangle ABC\)的面积平分的直线是什么样的．

考虑到\(a>0\)，该直线一定与线段\(BC\)相交，于是我们从\(BC\)上的一个动点\(M\)出发去构造平分\(\triangle ABC\)面积的直线．

根据动点\(M\)在\(BC\)中点的左上方还是右下方，三角形被分成的两部分形状不同，实际情况如下图如示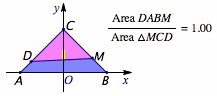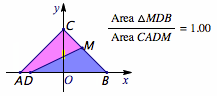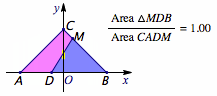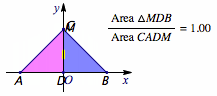： 实际上\(b\)的取值范围如图中线段所示（不包含端点）．

注一　由问题的对称性可知条件\(a>0\)是多余的．

注二    本题也可以直接代数计算解决，但计算量比较大．有兴趣的同学尝试．

赵晚龙老师提供了另外一种做法，见每日一题[279]的另解．