2009年北京市中考选择压轴题(2012年定西市中考选择压轴题):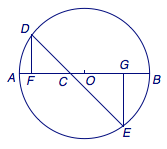
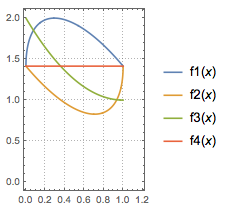
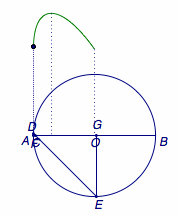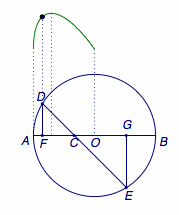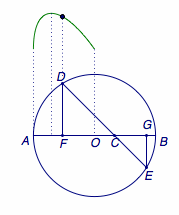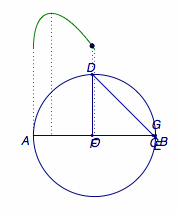
如图,\(C\)为\(\odot O\)直径\(AB\)上一动点,过点\(C\)的直线交\(\odot O\)于\(D\) 、 \( E \)两点,且\(\angle ACD=45^\circ\),\(DF\perp AB\) 于点\(F\),\( EG\perp AB \)于点\( G \),当点\( C \)在\( AB \)上运动时,设\( AF=x \),\( DE=y \),下列图象中,能表示\( y \)与\( x \)的函数关系式的图象大致是_______.
正确答案是\(f_1(x)\).
解 当\(F\)从\(A\)点出发时,显然有\(y\)随着\(x\)的增大而增大,因此只有\(f_1(x)\)符合题意.(也可以观察当\(C\)位于圆心\(O\)处时\(y\)取得最大值,于是函数有最大值,只有\(f_1(x)\)符合题意.)
因此这是一个“10秒钟解决”的选择压轴题,但之所以能够“10秒钟解决”并不是因为我们的解法精妙,而是题目实在太和谐了.于是我们尝试修复这个BUG:
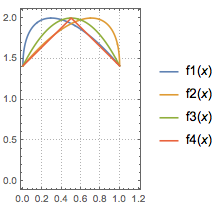
选项升级
定性分析
如图,可以确定函数的最大值点在定义域中点的左侧,因此选择\(f_1(x)\).
精确计算
不妨设圆的半径为\(1\),则可以计算得\[y=\sqrt 2\cdot\sqrt{x(2-x)}+\sqrt 2\left(1-x\right),\]于是令\[\begin{eqnarray}t=\sqrt{x(2-x)}-x,\end{eqnarray}\]则有\[\begin{eqnarray}y=\sqrt 2\cdot\left(t+1\right),\end{eqnarray}\]由(1)得\[2x^2+2(t-1)x+t^2=0,\]于是\[\Delta=4(t-1)^2-8t^2\geqslant 0,\]解得\[-1-\sqrt 2\leqslant t\leqslant -1+\sqrt 2,\]进而可得当\(x=1-\dfrac{\sqrt 2}2\)时,\(t\)取得最大值\(-1+\sqrt 2\).
因此再由(2)得\(y\)的最大值为\(2\),当\(x=1-\dfrac{\sqrt 2}{2}\)时取得.