来自 73Dsi 的非常漂亮的题目.
若对于任意三角形 $\triangle A B C$,曲线系 $\Gamma_m$ 中均存在其中一条曲线使得曲线上存在三点 $P,Q,R$ 且 $\triangle P Q R$ 与 $\triangle ABC$ 全等,则称该曲线系是保三角形曲线系.以下曲线系中是保三角形曲线系的有( )
A.$y=|mx|$($m\in\mathbb R$)
B.$x^2+y^2=m$($m>0$)
C.$y=x^m$($m\in\mathbb R$)
D.$y=m x^2$($m\in\mathbb R^{\ast}$)
E.$xy=m$($m\in\mathbb R^{\ast}$)
答案 ABCDE.
解析 对于选项 $\boxed{A}$,选择坐标原点 $O$ 为 $Q$,调节 $m$,使 $y=|m|x$($x\geqslant 0$)与 $y=-|m|x$($x\leqslant 0$)的夹角为 $\angle B$,然后在两条射线上分别取 $|QP|=|BA|,|QR|=|BC|$ 即可,选项正确;
对于选项 $\boxed{B}$,将 $\triangle ABC$ 放置在坐标平面上,并使坐标原点 $O$ 为其外心,调整 $m$ 使得圆 $\Gamma_m$ 为其外接圆,选项正确;
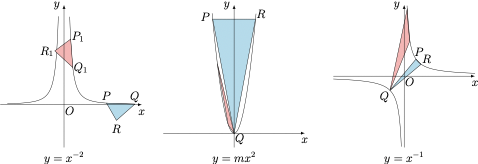
对于选项 $\boxed{C}$,取 $m=-2$,作与 $\triangle ABC$ 全等的 $\triangle PQR$,且 $PQ$ 是曲线在第一象限分支的弦,$R$ 在 $PQ$ 下方,则当 $PQ$ 足够远($x$ 轴正半轴方向)时,$R$ 在曲线在第二象限分支的外部;当 $PQ$ 向 $y$ 轴正半轴方向滑动时,由于曲线两支的距离可以要多近有多近,因此必然存在某个时刻使得 $R$ 在曲线在第二象限分支的内部,所以在滑动过程中存在某个时刻使 $R$ 落在曲线上,选项正确;
对于选项 $\boxed{D}$,不妨设 $\angle B$ 为锐角,取 $Q(0,0)$,作等腰三角形 $PQR$,使 $\angle PQR=\angle B$,考虑 $QP$ 趋于 $O$ 处切线(即 $x$ 轴),可得 $\dfrac{|QP|}{|QR|}$ 可以取遍 $(0,1]$,此时可以得到与 $\triangle ABC$ 相似的三角形,再利用 $m$ 调节大小使三角形全等,选项正确;
对于选项 $\boxed{E}$,不妨设 $\angle B$ 为锐角,考虑 $y=\dfrac 1x$,取 $Q(-1,-1)$,则 $\dfrac{|QP|}{|QR|}$ 可以取遍 $(0,1]$,此时可以得到与 $\triangle ABC$ 相似的三角形,再利用 $m$ 调节大小使三角形全等,选项正确;
综上所述,正确的选项为 $\boxed{A}$ $\boxed{B}$ $\boxed{C}$ $\boxed{D}$ $\boxed{E}$.
