在 \(\triangle ABC\) 中,角 \(A,B,C\) 所对的边为 \(a,b,c\),有\[\begin{split} a^2=&b^2+c^2-2bc\cos A,\\ b^2=&a^2+c^2-2ac\cos B,\\ c^2=&a^2+b^2-2ab\cos C.\end{split}\]
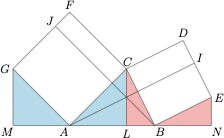
证明 如图,作正方形$BCDE$以及$ACFG$,作$AI\perp DE$于$I$,$BJ\perp FG$于$J$,点$C,G,E$在直线$AB$上的投影分别为$L,M,N$.
根据辅助线作法,有\[DI=b\cos C,FJ=a\cos C,\]于是\[\begin{split} a^2+b^2-2ab\cos C&=[BCDE]+[ACFG]-CD\cdot DI-CF\cdot FJ\\ &=2[\triangle BEI]+2[\triangle AGJ]\\ &=2[\triangle BEA]+2[\triangle AGB]\\ &=2[\triangle ABE]+2[\triangle ABG]\\ &=AB\cdot EN+AB\cdot GM\\ &=AB\cdot BL+AB\cdot AL\\ &=AB\cdot (BL+AL)\\ &=c^2.\end{split}\]