2025年高考全国II卷 #16
已知椭圆 $C: \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的离心率为 $\dfrac{\sqrt{2}}{2}$,长轴长为 $ 4$.
1、求 $C$ 的方程.
2、过点 $(0,-2)$ 的直线 $l $ 与 $ C $ 交于 $ A,B $ 两点,$ O $ 为坐标原点.若 $ {\triangle O A B} $ 的面积为 $ \sqrt{2} $,求 $ |A B|$.
解析
1、根据题意,有\[\begin{cases} \sqrt{1-\dfrac{b^2}{a^2}}=\dfrac{\sqrt 2}2,\\ 2a=4,\end{cases}\implies \begin{cases} a=2,\\ b=\sqrt 2,\end{cases}\]因此 $C$ 的方程为 $\dfrac{x^2}4+\dfrac{y^2}2=1$.
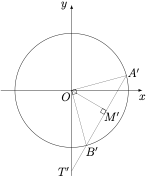
2、在伸缩变换 $x'=x$,$y'=\sqrt 2y$ 下,椭圆 $C$ 变为圆 $x^2+y^2=4$,设变换后点 $A,B$ 对应点为 $A',B'$,则\[[\triangle OA'B']=\sqrt 2\cdot [\triangle OAB]=2=\dfrac 12\cdot |OA'|\cdot |OB'|,\]因此 $\angle A'OB'=\dfrac{\pi}2$,$|A'B'|=2\sqrt 2$.记 $T(0,-2)$,$T'(0,-2\sqrt 2)$,$O$ 在 $A'B'$ 上的投影为 $M'$,则\[\begin{cases} |OT'|=2\sqrt 2,\\ |OM'|=\sqrt 2,\end{cases}\implies \angle OT'M'=\dfrac{\pi}6,\]因此直线 $l$ 变换后的斜率 $k'=\sqrt 3$,变换前的斜率 $k'=\dfrac{\sqrt{3}}{\sqrt 2}$,进而\[ |AB|=\dfrac{\sqrt{1+k^2}}{\sqrt{1+k'^2}}\cdot |A'B'|=\sqrt 5.\]