已知双曲线 $C: x^2-\dfrac{y^2}{24}=1$ 的左、右焦点分别为 $F_1,F_2$,$P$ 为双曲线 $C$ 第一象限上一点,$\angle F_1 PF_2$ 的角平分线为 $l$,过点 $O$ 作 $PF_2$ 的平行线,分别与 $PF_1,l$ 交于 $M,N$ 两点,若 $|MN|=\dfrac 2 3\left|PF_2\right|$,则 $\triangle PF_1 F_2$ 的面积为( )
A.$20$
B.$12$
C.$24$
D.$10$
答案 C.
解析 如图,由 $PN$ 平分 $\angle F_1PF_2$ 以及 $MN\parallel PF_2$ 可得\[\angle MPN=\angle NPF_2=\angle MNP\implies |MN|=|MP|,\]
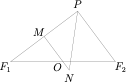
设 $|PF_2|=6m$,则 $|MN|=4m$,于是\[|MP|=|MN|=4m,\quad |MF_1|=|MP|=4m,\]从而由 $|PF_1|-|PF_2|=2$,可得 $2m=2$,于是 $m=1$,进而 $|PF_1|=8$,$|PF_2|=6$,$|F_1F_2|=10$,$\triangle PF_1F_2$ 的面积为 $24$.
