已知双曲线 $C=\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$($a>0$,$b>0$)的左、右焦点分别为 $F_1,F_2$,过 $F_1$ 作直线分别交双曲线的左、右两支于 $M,N$ 两点,满足 $\overrightarrow{NF_2}=2\overrightarrow{NP}$,且 $\overrightarrow{MP}\cdot\left(\overrightarrow{MF_2}-\overrightarrow{MN}\right)=0$,$\angle F_1 NF_2=\dfrac{\pi}3$,则双曲线 $C$ 的渐近线方程为( )
A.$y=\pm\sqrt 6 x$
B.$y=\pm\sqrt 7 x$
C.$y=\pm 2\sqrt 2 x$
D.$y=\pm 3 x$
答案 A.
解析 根据题意,由 $\overrightarrow{NF_2}=2\overrightarrow{NP}$,且 $\overrightarrow{MP}\cdot\left(\overrightarrow{MF_2}-\overrightarrow{MN}\right)=0$,$\angle F_1 NF_2=\dfrac{\pi}3$ 可得 $P$ 为 $NF_2$ 的中点,且 $MP\perp F_1F_2$,进而 $\triangle NMF_2$ 是等边三角形,如图.
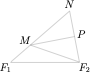
设 $\triangle NMF_2$ 的边长为 $2$,则\[|MN|=|MF_2|=|NF_2|=2\implies 2a=|NF_1|-|NF_2|=|MF_1|=|MF_2|-2a=2-2a,\]于是 $2a=1$,于是 $|NF_1|=3$,$|NF_2|=2$,根据余弦定理,可得\[|F_1F_2|=\sqrt{|NF_1|^2+|NF_2|^2-2\cdot |NF_1|\cdot |NF_2|\cdot \cos\angle F_1NF_2}=\sqrt 7,\]因此 $2b=\sqrt 6$,进而所求渐近线方程为 $y=\pm 6x$.
