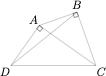
在不断发展的过程中,我国在兼顾创新创造的同时,也在强调已有资源的重复利用,废弃资源的合理使用,如土地资源的再利用是其中的重要一环.为了积极响应国家号召,某地计划将如图所示的四边形荒地 $ABCD$ 改造为绿化公园,并拟计划修建主干路 $AC$ 与 $BD$.为更好的规划建设,利用无人机对该地区俯视图进行角度勘探,在勘探简化图中,$AD\perp AC$,$AB\perp BC$,$AC$ 平分 $\angle BCD$,$BD=CD$,则 $\cos\angle ACD=$ ( )
A.$\dfrac{\sqrt 6}3$
B.$\dfrac{2\sqrt 2}9$
C.$\dfrac{2\sqrt 2}3$
D.$\dfrac{\sqrt 3}3$
答案 A.
解析 设 $\angle ACD=\theta$,$CD=1$,则\[AC=\cos\theta,\quad BC=\cos^2\theta,\]于是在 $\triangle BCD$ 中应用余弦定理,有\[BD^2=BC^2+CD^2-2\cdot BC\cdot CD\cdot \cos\angle BCD=\cos^4\theta+1-2\cos(2\theta)\cos^2\theta,\]又 $BD=CD=1$,从而\[\cos^4\theta+1-2\cos(2\theta)\cos^2\theta=1\iff \cos\theta=\dfrac{\sqrt 3}6.\]
