2025年1月湖北省武汉市高三数学调研考试 #14
在 $\triangle ABC$ 中,$BC=8$,点 $D$ 是 $BC$ 上的点 $,AD$ 平分 $\angle BAC$,$\triangle ABD$ 面积是 $\triangle ADC$ 面积的 $3$ 倍,当 $\triangle ABC$ 的面积最大时,$\sin\angle BAC=$ _____.
答案 $\dfrac 45$.
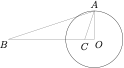
解析 根据题意,有\[[\triangle ABD]=3[\triangle ADC]\implies BD=3\cdot DC\implies AB=3\cdot AC,\]于是根据阿波罗尼斯圆定义,点 $A$ 的轨迹是以 $O$ 为圆心,$r$ 为半径的圆,其中\[\dfrac{OB}{r}=\dfrac{r}{OC}=3,\quad OB-OC=8,\]于是 $(OB,r,OC)=(9,3,1)$.当 $\triangle ABC$ 的面积最大时,有 $AO\perp BC$,此时\[\tan\angle BAC=\tan(\angle BAO-\angle CAO)=\dfrac{3-\frac 13}{1+3\cdot \frac 13}=\dfrac 43,\]于是 $\sin\angle BAC=\dfrac 45$.