每日一题[3774]切面分析

2025年4月湖北省武汉市高三数学调研考试 #14

在各棱长均相等的正四面体 $PABC$ 中，取棱 $PC$ 上一点 $T$，使 $PT=2 TC$，连接 $TA,TB$，三棱锥 $T-PAB$ 的内切球的球心为 $M$，三棱锥 $T-ABC$ 的内切球的球心为 $N$，则平面 $MAB$ 与平面 $NAB$ 的夹角的正弦值是_____．

答案    $\dfrac{\sqrt3}3$．

解析    设 $AB$ 的中点为 $Q$，则 $M,N$ 均在截面 $PQC$ 中，且 $M,N$ 分别在 $\angle TQP,\angle TQC$ 的平分线 $QU,QV$ 上，如图．

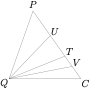
于是平面 $MAB$ 与平面 $NAB$ 的夹角的正弦值为 $$\sin\angle UQV=\sin\dfrac 12\angle PQC=\dfrac{\frac 12|PC|}{|PQ|}=\dfrac{\sqrt3}3.$$