已知椭圆 $C: \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的离心率为 $\dfrac{1}{2}$,且经过点 $M(-2,0)$,$F_1, F_2$ 为椭圆 $C$ 的左、右焦点.$A(x_1,y_1),B(x_2,y_2)$ 是椭圆上两点,直线 $AF_1,BF_2$ 相交于点 $Q(x_0,y_0)$.
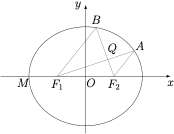
1、求椭圆 $C$ 的标准方程;
2、① 若 $A F_2\parallel B F_1$,证明:$\dfrac{1}{y_1}+\dfrac{1}{y_2}=\dfrac{1}{y_0}$;
② 若 $\left|Q F_1\right|+\left|Q F_2\right|=3$,探究 $y_0, y_1, y_2$ 之间的关系.
解析
1、根据题意,有\[\begin{cases} \sqrt{1-\dfrac{b^2}{a^2}}=\dfrac 12,\\ a=2,\end{cases}\iff \begin{cases} a^2=4,\\ b^2=3,\end{cases}\]于是椭圆 $C$ 的标准方程为 $\dfrac{x^2}4+\dfrac{y^2}3=1$.
2、① 根据题意,有 $\triangle AQF_2$ 与 $\triangle ABF_1$ 相似,于是\[\dfrac{y_0}{y_1}+\dfrac{y_0}{y_1}=\dfrac{|QF_1|}{|AF_1|}+\dfrac{|QF_2|}{|BF_2|}=\dfrac{|QF_1|}{|AF_1|}+\dfrac{|QA|}{|AF_1|}=1.\]
② 根据题意,$Q$ 在椭圆 $\dfrac{4x^2}{9}+\dfrac{4y^2}{5}=1$ 上运动,设 $|QF_1|=m$,$|QF_2|=n$,则根据余弦定理,有\[\cos\angle QF_1F_2=\dfrac{m^2+(2c)^2-n^2}{2\cdot m\cdot 2c}=\dfrac{m^2-n^2+4c^2}{4cm},\]于是根据焦半径公式,有\[|AF_1|=\dfrac{b^2}{a-c\cos\angle AF_1F_2}=\dfrac{4b^2m}{4am-m^2+n^2-4c^2},\]因此\[\begin{split}\dfrac{y_0}{y_1}+\dfrac{y_0}{y_1}&=\dfrac{|QF_1|}{|AF_1|}+\dfrac{|QF_2|}{|BF_2|}\\ &=\dfrac{4am-m^2+n^2-4c^2}{4b^2}+\dfrac{4an-n^2+m^2-4c^2}{4b^2} \\ &=\dfrac{a(m+n)-2c^2}{b^2}\\ &=\dfrac 43,\end{split}\]即 $\dfrac{1}{y_1}+\dfrac{1}{y_2}=\dfrac 4{3y_0}$.
