每日一题[277] 一体三化

2014年湖南省十三校联考二模试题（原题为选择题）：

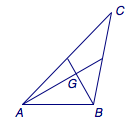
已知$G$是$\triangle ABC$的重心，且$AG\perp BG$，$\dfrac{1}{\tan A}+\dfrac{1}{\tan B}=\dfrac{\lambda }{\tan C}$，则实数$\lambda=$_______．

---

 

正确答案是$\dfrac 12$．

首先简化含$\lambda$的表达式：$$\begin{split}\lambda&=\dfrac{\sin C}{\cos C}\cdot\left(\dfrac{\cos A}{\sin A}+\dfrac{\cos B}{\sin B}\right)\\&=\dfrac{\sin^2C}{\sin A\cdot\sin B\cdot \cos C}\\&=\dfrac{c^2}{ab\cos C}.\end{split} $$

接下来处理核心条件$AG\perp BG$．

法一    利用向量的数量积

记$\overrightarrow {CA}=\overrightarrow m$，$\overrightarrow {CB}=\overrightarrow n$，则$\overrightarrow {CG}=\dfrac 13\overrightarrow m+\dfrac 13\overrightarrow n$，于是$$\begin{split} \overrightarrow {AG}\cdot \overrightarrow {BG}&=\left(\overrightarrow {CG}-\overrightarrow {CA}\right)\cdot\left( \overrightarrow {CG}-\overrightarrow {CB}\right)\\&=\left(-\dfrac 23\overrightarrow m+\dfrac 13\overrightarrow n\right) \cdot\left(\dfrac 13\overrightarrow m-\dfrac 23\overrightarrow n\right)\\&=-\dfrac 19\left( 2\overrightarrow m\cdot \overrightarrow m+2\overrightarrow n\cdot \overrightarrow n-5\overrightarrow m\cdot\overrightarrow n\right)\\&=-\dfrac 19\left(2a^2+2b^2-5ab\cos C\right),\end{split}$$于是$$\lambda=\dfrac{a^2+b^2-2ab\cos C}{ab\cos C}=\dfrac 12.$$

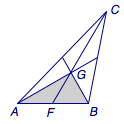
法二    将直角转化为边关系

连接$CG$并延长交$AB$于$F$，则$$CF=3GF=\dfrac 32c,$$对$\triangle ABC$应用中线定理，有$$\begin{split} a^2+b^2&=2\left(CF^2+BF^2\right)\\&=2\left(\dfrac 94c^2+\dfrac 14c^2\right)\\&=5c^2,\end{split} $$而$$\lambda=\dfrac{c^2}{ab\cos C}=\dfrac{2c^2}{a^2+b^2-c^2}=\dfrac 12.$$

法三    利用勾股定理

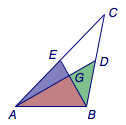
分别延长$AG$至$D$，延长$BG$至$E$，设$AG=2GD=2m$，$BG=2GE=2n$．

在$\triangle ABG$，$\triangle AEG$，$\triangle BDG$中应用勾股定理，有$$\begin{split} &4m^2+4n^2=c^2,\\&\dfrac 14b^2=4m^2+n^2,\\&\dfrac 14a^2=4n^2+m^2,\end{split} $$从而$$a^2+b^2=5c^2,$$以下略．

（当然，也可以以$G$为原点，$GA$、$GB$为正方向建立平面直角坐标系，然后利用两点间的距离公式计算．）

总结    通过正余弦定理将$\lambda$由复杂的角关系转化为简单的边关系之后，如何将核心条件$AG\perp BG$转化为边关系就是解决问题的核心了．

---

注    法二、法三来自QQ群，中国数学解题研究会．

2015年10月26日补充一种独立解法．

如图，记$\angle EAG=\alpha$，$\angle GAB=\beta$，$\angle GBA=\gamma $，则$$\tan\alpha=\dfrac{EG}{AG}=\dfrac 12\cdot\dfrac{GB}{AG}=\dfrac 12\tan\beta,$$记$\tan\beta =t$，则$$\tan A=\tan(\alpha+\beta)=\dfrac{3t}{2-t^2}.$$

注意到$\beta+\gamma=90^\circ$，于是类似的可得$$\tan B=\dfrac{3\cdot \frac {1}{t}}{2-\left(\frac {1}{t}\right)^2}=\dfrac{3t}{2t^2-1}.$$

另一方面，有$$\begin{split} \lambda&=-\tan(A+B)\cdot \left(\dfrac{1}{\tan A}+\dfrac{1}{\tan B}\right)\\&=-\dfrac{\left(\tan A+\tan B\right)^2}{\tan A\cdot\tan B\cdot\left(1-\tan A\cdot \tan B\right)},\end{split} $$将$\tan A$和$\tan B$的值代入运算得$$\lambda =\dfrac 12.$$