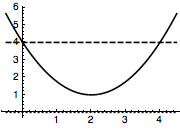
问题1 已知不等式\(a\leqslant \dfrac 34x^2-3x+4\leqslant b\)的解集恰好是\([a,b]\),求\(a,b\)的值.
问题2 已知函数\(f(x)=\dfrac 34x^2-3x+4\)的定义域和值域都是\([a,b]\),求\(a,b\)的值.
正确答案是(1)\(a=0,b=4\);(2)\(a=1,b=4\).
解 相同的函数\(f(x)=\dfrac 34x^2-3x+4\),不同的问题,但出发点都是函数的图象.
问题1 题中不等式的解是函数\(f(x)=\dfrac 34x^2-3x+4\)的图象在直线\(y=a\)与直线\(y=b\)之间的部分在\(x\)轴上的投影所表示的区间.
容易确定\(a\leqslant 1\),否则投影区间不连续,与题意不符.
于是\(a,b\)是方程\(f(x)=b\)的两根,根据韦达定理,有\[\begin{cases}a+b=4,\\ab=\dfrac 43(4-b),\end{cases}\]解得\[a=0\land b=4.\]
问题2 这个问题可以在问题1的基础上继续思考,设函数\(f(x)=\dfrac 34x^2-3x+4\)的图象在直线\(y=a\)与直线\(y=b\)之间的部分在\(x\)轴上的投影所表示的区间为\(D\),那么定义域\([a,b]\)需要满足必要条件\([a,b]\subseteq D\).
若$[a,b]$为$f(x)$的单调递减区间,则有\[\begin{cases} a=f(b)=\dfrac 34b^2-3b+4,\\b=f(a)=\dfrac 34a^2-3a+4,\end{cases} \]两式相减整理得$a+b=\dfrac 83$,代回方程组中解得$a=b=\dfrac 43$.不符合题意;
若$[a,b]$为$f(x)$的单调增区间,则有$$\begin{cases} f(a)=a,\\f(b)=b,\end{cases}$$解得$a=\dfrac 43,b=4$,与单调性的前提不相符,舍去;
若$f(x)$在$[a,b]$上不单调,则$2\in [a,b]$,从而有$a=1,b\geqslant 2$,所以$b$满足$f(b)=b$,解得$b=4$.
综上,符合题意的$a,b$的值为$a=1\land b=4$.
注 这个问题是我从江苏苗勇老师的博客中看到的.