已知,如图\(BD\perp AC\),\(\angle AEC=45^\circ\),\(BD=2CE\),\(DE\parallel BC\),求证\(CE=AC+AD\).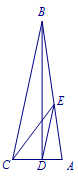
解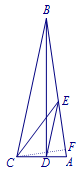 作\(CF\perp AB\)交\(AB\)于点\(F\). 设\(CE=a\),\(AD=x\),所以\[BD=2a,EF=CF=\dfrac{\sqrt 2}{2}a.\]
作\(CF\perp AB\)交\(AB\)于点\(F\). 设\(CE=a\),\(AD=x\),所以\[BD=2a,EF=CF=\dfrac{\sqrt 2}{2}a.\]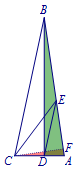 因为\(\triangle CAF\backsim \triangle BAD\), 所以\[\dfrac{AC}{AB}=\dfrac{AF}{AD}=\dfrac{CF}{BD}=\dfrac{\sqrt 2}{4},\]所以\[AF=\dfrac{\sqrt 2}{4}x,AC=\sqrt{\dfrac 18x^2+\dfrac 12a^2}.\]
因为\(\triangle CAF\backsim \triangle BAD\), 所以\[\dfrac{AC}{AB}=\dfrac{AF}{AD}=\dfrac{CF}{BD}=\dfrac{\sqrt 2}{4},\]所以\[AF=\dfrac{\sqrt 2}{4}x,AC=\sqrt{\dfrac 18x^2+\dfrac 12a^2}.\]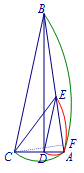 因为\(DE\parallel BC\),所以\[\dfrac{AD}{AC}=\dfrac{AE}{AB},\] 所以\[\begin{split} AD & =\dfrac{AC}{AB}\times AE\\ &=\dfrac{\sqrt 2}{4}(EF+AF)\\ &=\dfrac{\sqrt 2}{4}(\dfrac{\sqrt 2}{2}a+\dfrac{\sqrt 2}{4}x)\\ &=x.\end{split}\]解得\[x=\dfrac 27a,AC=\dfrac 57 a.\]所以\[CE=AD+AC.\]
因为\(DE\parallel BC\),所以\[\dfrac{AD}{AC}=\dfrac{AE}{AB},\] 所以\[\begin{split} AD & =\dfrac{AC}{AB}\times AE\\ &=\dfrac{\sqrt 2}{4}(EF+AF)\\ &=\dfrac{\sqrt 2}{4}(\dfrac{\sqrt 2}{2}a+\dfrac{\sqrt 2}{4}x)\\ &=x.\end{split}\]解得\[x=\dfrac 27a,AC=\dfrac 57 a.\]所以\[CE=AD+AC.\]

长见识了!