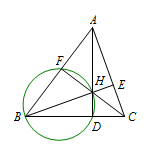
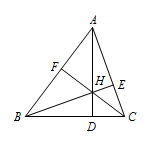
如图，锐角\(\triangle ABC\)的垂心为\(H\)，三条高的垂足分为\(D,E,F\)，则\(H\)是\(\triangle DEF\)的\(\underline{\qquad}\)心．
答案 内心
分析 三角形的垂心是三角形三边高所在的直线的交点，常用来判定四点共圆以及构造三角形相似．
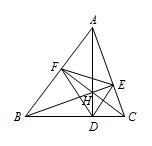
如图所示，由\(H\)为\(\triangle ABC\)的垂心，易得\(A,E,H,F\)四点共圆，则\[\angle HAE=\angle HFE,\ \angle FAH=\angle FEH;\]同理可得\[\angle HBD=\angle HFD,\ \angle FBH=\angle FDH;\\ \angle HCD=\angle HED,\ \angle ECH=\angle EDH.\]亦由\(H\)为\(\triangle ABC\)的垂心，可得\(\triangle HAE \sim \triangle HBD\)，则\[\angle HAE=\angle HBD;\]同理可得\[\angle FAH=\angle HCD;\ \angle FBH=\angle ECH.\]
\(\therefore \angle DFH=\angle EFH\)，\(\angle FDH=\angle EDH\)，\(\angle DEH=\angle FEH\)．
\(\therefore H\)为\(\triangle DEF\)的内心．
注 由本题可得：锐角三角形的垂心是其垂足三角形的内心．
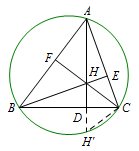
练习1 求证：三角形垂心关于边的对称点在外接圆上．
提示 如图所示，延长\(AD\)交\(\triangle ABC\)外接圆于点\(H'\)，则\[\triangle AH'C=\angle ABC=\angle ABE+\angle CBE=\angle ACF+\angle CAD=\angle CHH',\]所以\(CH=CH'\)，即得证．
练习2 如图，设锐角\(\triangle ABC\)的三条高\(AD,BE,CF\)相交于\(H\)，若\(BC=a\)，\(AC=b\)，\(AB=c\)，则\(AH \cdot AD+BH \cdot BE +CH \cdot CF\)的值为\(\underline{\qquad}\)．
答案 \(\dfrac 12\left(a^2+b^2+c^2\right)\)．
提示 如图由\(B,D,H,F\)四点共圆以及圆幂定理，可得\[AF \cdot AB=AH \cdot AD;\]同理可得\[\begin{split}&AH \cdot AD=AE \cdot AC;\\&CE \cdot CA=CH \cdot CF=CD \cdot CB;\\&BD \cdot BC=BH \cdot BE=BF \cdot BA.\end{split}\]从而得到\[AH \cdot AD+BH \cdot BE +CH \cdot CF=\dfrac 12\left(a^2+b^2+c^2\right).\]