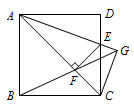
如图，在正方形\(ABCD\)中，点\(E\)为\(CD\)上任意一点，\(EF⊥AC\)于点\(F\)，\(BF\)与\(AE\)的延长线交于点\(G\)，连接\(CG\)，则\(\angle BGC=\)____．
正确答案是\(45^\circ\)．
解 如图所示，由题意可得\(A,D,E,F\)四点共圆．
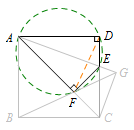连接\(DF\)，则\[\angle FAE=\angle FDE=\angle GBC.\]
可得\(A,B,C,G\)四点共圆．
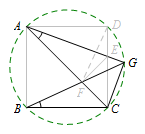所以\[\angle BGC=\angle BAC=45^\circ.\]
注 常见的四点共圆基本图形有：
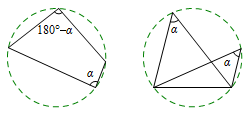
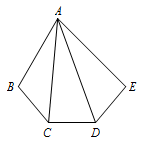
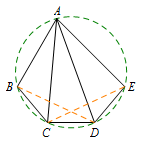
练习 如图，已知在凸五边形\(ABCDE\)中，\(\angle BAE=3\alpha\)，\(BC=CD=DE\)，且\(\angle BCD=\angle CDE=180^\circ-2\alpha\)．求证：\(\angle BAC=\angle CAD=\angle DAE\)．
提示 如图，连接\(BD,CE\)，证\(A,B,C,D,E\)五点共圆即可．