每日一题[225] 利用边界条件解题

2015年高考全国卷I 理科数学第5题：

已知$M(x_0,y_0)$是双曲线$C:\dfrac {x^2}{2}-y^2=1$上的一点，$F_1$、$F_2$是$C$的两个焦点，若$\overrightarrow  {MF_1}\cdot \overrightarrow  {MF_2}<0$，则$y_0$的取值范围是（        ）

A．$\left(-\dfrac {\sqrt {3}}{3},\dfrac {\sqrt {3}}{3}\right)$

B．$\left(-\dfrac {\sqrt {3}}{6},\dfrac {\sqrt {3}}{6}\right)$

C．$\left(-\dfrac {2\sqrt {2}}{3},\dfrac {2\sqrt {2}}{3}\right)$

D．$\left(-\dfrac {2\sqrt {3}}{3},\dfrac {2\sqrt {3}}{3}\right)$

---

正确答案是A．

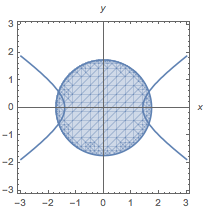
解    考虑条件$\overrightarrow  {MF_1}\cdot \overrightarrow  {MF_2}<0$边界情形为$\overrightarrow  {MF_1}\cdot \overrightarrow  {MF_2}=0$，几何意义为点$M$的轨迹是以$F_1$、$F_2$为直径端点的圆．进而可知符合题意的点$M$均在圆内，如图．

接下来用两种方式去计算双曲线在圆内的曲线段端点的纵坐标．

方式一    利用轨迹方程

联立圆和双曲线的轨迹方程

$$\begin{cases}x^2+y^2=3,\\\dfrac{x^2}2-y^2=1,\end{cases}$$ 解得 $$y=\pm\dfrac{\sqrt 3}3.$$

方式二    利用焦点三角形面积公式

根据双曲线的焦点三角形面积公式，有

$$S_{\triangle MF_1F_2}=1^2\cdot\cot{\dfrac{90^\circ}2}=1,$$ 另一方面，三角形$MF_1F_2$的底$F_1F_2$的长为$2\sqrt 3$，于是可得其边$F_1F_2$上的高为$\dfrac{\sqrt 3}3$．

因此可得所求$y_0$的取值范围是$\left(-\dfrac{\sqrt  3}{3},\dfrac{\sqrt 3}{3}\right)$．

---

注    以双曲线上一点与两个焦点构成的三角形称为焦点三角形，焦点三角形的面积$S$与两个焦点形成线段所对的角$\theta$之间具有数量关系

$$S=b^2\cdot\cot\dfrac{\theta}2,$$ 其中$b$为双曲线的半虚轴长．

椭圆也有类似的结论，以椭圆上一点与两个焦点构成的三角形面积$S$与两个焦点形成线段所对的角$\theta$之间具有数量关系

$$S=b^2\cdot\tan\dfrac{\theta}2,$$ 其中$b$为椭圆的半短轴长．

双曲线的焦点三角形面积公式和椭圆的焦点三角形面积公式合称焦点三角形面积公式．焦点三角形面积公式是利用焦点三角形处理几何问题的重要桥梁．