已知双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$($a>0,b>0$)的左、右焦点分别为 $F_1,F_2$,以右焦点 $F_2$ 为焦点的抛物线 $y^2=2px$($p>0$)与双曲线交于第一象限的 $P$ 点,若 $|PF_1|+|PF_2|=3|F_1F_2|$,则双曲线的离心率 $e=$ ( )
A.$2$
B.$5$
C.$\dfrac {\sqrt 2+1}2$
D.$\dfrac {\sqrt 5+1}2$
答案 A.
解析 如图,设抛物线的准线为 $l$,则 $l$ 过双曲线的左焦点 $F_1$,设 $P$ 在 $l$ 上的投影为 $H$,则根据抛物线的定义,有 $|PF_1|=|PH|$.
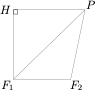
由 $|F_1F_2|=p$,$|PF_1|+|PF_2|=3|F_1F_2|$,结合双曲线的定义,可得\[|PF_1|=\dfrac32p+a,\quad |PF_2|=\dfrac 32p-a,\]进而在直角三角形 $PHF_1$ 中,可得 $P$ 点纵坐标的平方为\[|HF_1|^2=|PF_1|^2-|PH|^2=|PF_1|^2-|PF_2|^2=6pa,\]而 $P$ 点横坐标为\[|PH|-|F_1F_2|=p-a,\]从而\[6pa=2p(p-a)\implies p=4a,\]因此双曲线的离心率 $e=\dfrac{|F_1F_2|}{2a}=\dfrac{p}{2a}=2$.
