已知三棱锥 $P-ABC$ 的四个顶点在球 $O$ 的球面上,$PA=PB=PC$,$\triangle ABC$ 是边长为 $2$ 的正三角形,$E,F$ 分别是 $PA,AB$ 的中点,$\angle CEF=90^\circ$,则球 $O$ 的体积为( )
A.$8\sqrt 6\pi$
B.$4\sqrt 6\pi$
C.$2\sqrt 6\pi$
D.$\sqrt 6\pi$
答案 D.
解析 如图,设 $PA=a$.
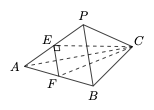
在 $\triangle PAC$ 中,应用平行四边形的性质可得\[4CE^2+PA^2=2AC^2+2PC^2\implies 4CE^2=a^2+8,\]在 $\triangle CEF$ 中应用勾股定理,可得\[CE^2+EF^2=CF^2\implies 4CE^2=12-a^2,\]因此 $a=\sqrt 2$,进而 $\angle APB=\angle BPC=\angle CPA=90^\circ$,所以四面体 $PABC$ 的外接平行六面体为棱长为 $\sqrt 2$ 的正方体,其外接球直径 $d$ 为该正方体的体对角线长,为 $\sqrt 6$,因此球 $O$ 的体积为 $\dfrac 16\pi d^3=\sqrt 6\pi$.
