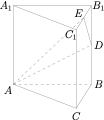
在各棱长均为 $1$ 的正三棱柱 $ABC-A_1 B_1 C_1$ 中,$D,E$ 分别为 $BB_1,B_1 C_1$ 的中点,过 $A,D,E$ 三点的截面将三棱柱分成上下两部分,记体积较小部分的体积为 $V_1$,另一部分的体积为 $V_2$,则 $\dfrac{V_1}{V_2}$ 的值为( )
A.$\dfrac{13}{21}$
B.$\dfrac{13}{23}$
C.$\dfrac 3 5$
D.$\dfrac 9{11}$
答案 B.
解析 如图,在平面 $BB_1C_1C$ 中,延长 $DE$ 分别与直线 $CB,CC_1$ 交于点 $M,N$,则\[|MB|=|NC_1|=\dfrac 12,\]
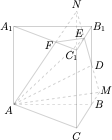
于是\[\begin{split} [ABCDEFC_1]&=[EFC_1-MAC]-[D-ABM]\\ &=\dfrac {26}{27}[N-MAC]-\dfrac1{9}[N-MAC]\\ &=\dfrac {23}{27}[N-MAC]\\ &=\dfrac {23}{27}\cdot \left(\dfrac 13\cdot \dfrac 32|CC_1|\cdot \dfrac 32[ABC]\right)\\ &=\dfrac{23}{36}[ABC-A_1B_1C_1],\end{split}\]于是 $\dfrac{V_1}{V_2}=\dfrac{13}{23}$.
