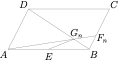
如图,已知点 $E$ 是 $ABCD$ 的边 $AB$ 的中点,$F_n$($n\in \mathbb N^{\ast}$)为边 $BC$ 上的一列点,连接 $AF_n$ 交 $BD$ 于 $G_n$,点 $G_n$($n\in\mathbb N^{\ast}$)满足 $\overrightarrow{G_n D}=a_{n+1}\cdot\overrightarrow{G_n A}-2\left(2 a_n+3\right)\cdot\overrightarrow{G_n E}$,其中数列 $\left\{a_n\right\}$ 是首项为 $1$ 的正项数列,$S_n$ 是数列 $\left\{a_n\right\}$ 的前 $n$ 项和,则下列结论正确的有[[nn]]
A.$a_3=13$
B.数列 $\left\{a_n+3\right\}$ 是等比数列
C.$a_n=4 n-3$
D.$S_n=2^{n+2}-3 n-4$
答案 ABD.
解析 将题中等式改写为以 $B$ 为起点的,有\[ \overrightarrow{BD}-\overrightarrow{BG_n}=a_{n+1}\left(\overrightarrow{BA}-\overrightarrow{BG_n}\right)-2(2a_n+3)\left(\overrightarrow{BE}-\overrightarrow{BG_n}\right),\]整理可得\[ (a_{n+1}+4a_n+5)\overrightarrow{BG_n}+\overrightarrow{BD}=(a_{n+1}-2a_n-3)\overrightarrow{BA},\]由于 $\overrightarrow{BG_n}$ 与 $\overrightarrow{BD}$ 共线,于是\[a_{n+1}-2a_n-3=0\implies a_{n+1}+3=2(a_n+3),\]结合 $a_1=1$,可得 $a_n=2^{n+1}-3$($n\in\mathbb N^{\ast}$),进而 $S_n=2^{n+2}-3n-4$($n\in\mathbb N^{\ast}$). 综上所述,正确的选项有 $\boxed{A}$ $\boxed{B}$ $\boxed{D}$.
