在平面四边形 $ABCD$ 中,$AB\perp AD$,$\angle ADC=4\angle ACD=120^{\circ}$,$CD=2$,$\triangle ABC$ 的面积为 $3\sqrt 3$,将 $\triangle ABD$ 沿 $BD$ 翻折至 $\triangle PBD$,其中 $P$ 为动点.

1、证明:三棱锥 $P-BCD$ 外接球的体积为定值;
2、当点 $C$ 到平面 $PBD$ 的距离为 $\dfrac{2\sqrt 6}3$,求直线 $PB$ 与直线 $CD$ 所成角的余弦值.
解析
1、根据题意,有\[\angle CAD=\angle ADC-\angle ACD=30^{\circ},\quad \angle CAB=\angle DAB-\angle CAD=60^{\circ},\]在 $\triangle ACD$ 内,由正弦定理得\[\dfrac{CD}{\sin\angle CAD}=\dfrac{AC}{\sin\angle ADC}\implies AC=2\sqrt 3,\]结合 $\triangle ABC$ 的面积\[[\triangle ABC]=3\sqrt 3\implies \dfrac 1 2 AB\cdot AC\sin\angle CAB=3\sqrt 3\implies AB=2\sqrt 3,\]于是 $\triangle ABC$ 为正三角形,进而可得 $\angle BCD$ 为直角,因此 $BD$ 的中点 $M$ 在翻折过程中到 $A,B,C,D$ 的距离相等,进而三棱锥 $P-BCD$ 外接球的球心为 $M$,半径为 $\dfrac 12BD=2$ 为定值,所以其体积为定值 $\dfrac{32\pi}3$.
2、如图,$M$ 为 $BD$ 的中点,$CN\perp BD$ 于 $N$.根据对称性,$C$ 到平面 $PBD$ 的距离与 $P$ 到平面 $BCD$ 的距离相同,设 $P$ 在 $BCD$ 上的投影为 $O$,则 $O$ 在直线 $CN$ 上,$NP=\sqrt 3$,$PO=\dfrac{2\sqrt 6}3$,从而\[ ON=\sqrt{ON^2-PO^2}=\dfrac{1}{\sqrt 3},\]
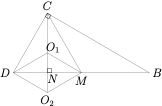
因此 $O$ 可能有两个位置(分别在 $BD$ 的两侧),记为 $O_1,O_2$.此时\[(PB,CD,PC,BD,PD,BC)=(2\sqrt 3,2,2,4,2,2\sqrt 3),(2\sqrt 3,2,2\sqrt 2,4,2,2\sqrt 3),\]根据空间余弦定理,所求余弦值为\[\dfrac{\left|(PC^2+BD^2)-(PD^2+BC^2)\right|}{2\cdot PB\cdot CD}=\dfrac{\sqrt 3}6,\text{或},\dfrac{\sqrt 3}3.\]
