定义\(\max\{a,b\}=\begin{cases}a,a\geqslant b,\\b,a<b,\end{cases}\)设实数\(x,y\)满足约束条件\(\begin{cases}|x|\leqslant 2,\\|y|\leqslant 2,\end{cases}\)则\(z=\max\{4x+y,3x-y\}\)的取值范围是______.
法一
如图,根据题意\[z=\begin{cases}4x+y,&x+2y\geqslant 0,\\3x-y,&x+2y<0,\end{cases}\]于是可以将可行域\(ABCD\)划分为两部分:梯形\(ABEF\)以及梯形\(EFDC\).这两个部分的目标函数分别为\(z=4x+y\)以及\(z=3x-y\).
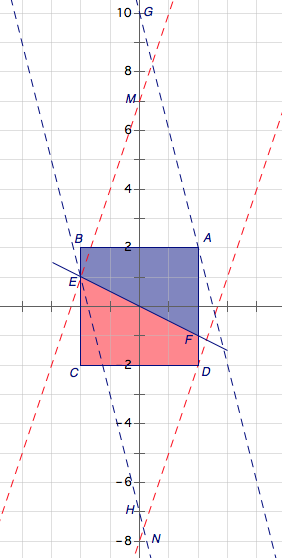
作图可知,从前一部分得到的\(z\)的取值范围为\([7,10]\);从后一部分得到的\(-z\)的取值范围是\([-8,7]\).取两个部分的并集,可得\(z\)的取值范围是\([-7,10]\).
法二
根据题意,\(z_{\max}\)为\(\max\{4x+y\}\)和\(\max\{3x-y\}\)中的较大者,事实上\[4x+y\leqslant 4|x|+|y|\leqslant 10,\]等号当且仅当\(x=y=2\)时取得;而\[3x-y\leqslant 3|x|+|y|\leqslant 8,\]等号当且仅当\(x=2,y=-2\)时取得.因此\(z_{\max}=10\).
另一方面,有\[z=\max\{4x+y,3x-y\}\geqslant \dfrac 12(4x+y)+\dfrac 12(3x-y)=\dfrac 72x\geqslant -7,\]等号当且仅当\(x=-2,y=1\)时取得.因此\(z_{\min}=-7\).
综上,\(z\)的取值范围是\([-7,10]\).

