2015年北京市人大附中高二期中复习题(原题为选择题):
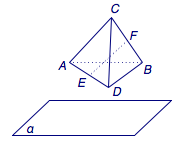
正四面体$ABCD$的棱长为$1$,平面$\alpha$是与棱$AB$平行的平面,$E$、$F$分别是棱$AD$和$BC$的中点,以$AB$为轴将正四面体$ABCD$旋转一周,线段$EF$在平面$\alpha$上的射影$E_1F_1$长的范围是_______.
正确答案是$\left[\dfrac 12,\dfrac{\sqrt 2}2\right]$.
解 可以直接通过一些特殊位置确定$EF$的长度的取值范围是$\left[\dfrac{\sqrt 2}2EF,EF\right]$,但严格求解的难度不小.我们可以通过一些常见的转化来将这个复杂的问题逐步简化.
第一步转化,正四面体的问题往往可以在其“外接正方体”中研究,这样更有利于数量和位置关系的推断,如图1.
由于研究的是线段$EF$在平面$\alpha$上的投影,因此可以取$\alpha$为底面$AB$.同时,正四面体绕$AB$转动,可以转化为底面$AB$绕直线$AB$转动.容易计算得$EF=\dfrac{\sqrt 2}2$,于是问题的关键就是在转动中$EF$与平面$\alpha$形成的线面角的取值范围.
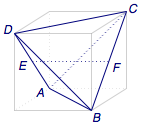
第二步转化,在平面$\alpha$的旋转过程中需要探索的线面角难以研究,因此将其转化为平面$\alpha$的法线与$EF$形成的线线角的取值范围,如图2.
此时,平面$\alpha$的法线可以取遍正四面体的外接正方体的包含$CD$的对角面内的直线.
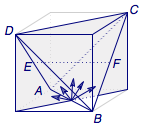
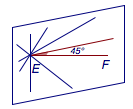
然后从复杂的图形中将相关部分提炼出来.我们知道,$EF$与对角面所成的角为$\dfrac {\pi} 4$,因此,平面$\alpha$的法线与$EF$的线线角的取值范围是$\left[\dfrac {\pi} 4,\dfrac {\pi} 2\right]$,如图3.
因此转动中$EF$与平面$\alpha$形成的线面角的取值范围是$\left[0,\dfrac {\pi} 4\right]$,于是所求的投影$E_1F_1$的取值范围是$\left[\dfrac 12,\dfrac{\sqrt 2}2\right]$.
在立体几何问题的解决过程中,掌握一些常见的转化手法(如同太极云手),就可以将问题逐步转化为简单而容易解决的问题,达到举重若轻的效果了.