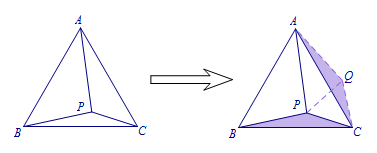
如图，等边\(\triangle ABC\)内有一点\(P\)，\(PC>PB\)，若\(\angle BPC=150^\circ\)，\(PA=5\)，\(S_{\triangle PBC}=3\)，求\(S_{\triangle ABC}\)．
证明 如图，将\(\triangle CBP\)绕点\(C\)顺时针旋转\(60^\circ\)到\(\triangle CAQ\)，连接\(PQ\)．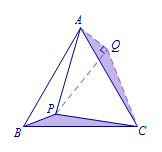
易知\(\triangle CPQ\)为等边三角形，\(\angle CQP=60^\circ\)，\(\angle AQP=90^\circ\)．
设\(BP=a\)，\(PC=b\)，则\(AQ=PB=a\)，\(PQ=PC=b\)．
在\(\mathrm {Rt}\triangle APQ\)中，根据勾股定理，得\[\begin{eqnarray}a^2+b^2=25.\end{eqnarray}\]
延长\(BP\)交\(CQ\)于点\(H\)，则\(PH\perp CQ\)，所以\(CH=\dfrac b2\)．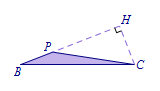
而\(S_{\triangle PBC}=\dfrac 12 BP\cdot CH=\dfrac 12\times a\times {\dfrac b2}=3\)，则\[\begin{eqnarray}ab=12. \end{eqnarray}\]在\(\mathrm {Rt}\triangle BCH\)中，根据勾股定理，得\[\begin{eqnarray}{BC}^2=\left( a+\dfrac {\sqrt 3b}2\right )^2+\left(\dfrac b2\right)^2=a^2+b^2+\sqrt 3ab.\end{eqnarray}\]
综合 (1)(2)(3)，得\[BC^2=25+12\sqrt 3.\]
所以\[S_{\triangle ABC}=\dfrac {\sqrt 3}4BC^2=\dfrac {25}4\sqrt 3+9.\]
由题我们可以看出，有的时候结合问题不需要解方程，运用整体带入的方法更省时省力.
综上，已知等边三角形\(ABC\)内一点\(P\)，无论是已知\(PA、PB、PC\)的长求解三角形还是求这三条线段的长类似的问题，通常我们利用旋转的办法将\(PA、PB、PC\)集中到一个三角形\(APQ\)中．实现从“Y”到“△”的转化．