2025年广东深圳宝安区一模数学试卷 #11
已知函数 $f(x)$ 为 $\mathbb R$ 上的奇函数,当 $0\leqslant x\leqslant 2$ 时,$f(x)=x^3-3 x$,且 $f(x)$ 的图象关于点 $(2,2)$ 中心对称,则下列说法正确的是( )
A.$f(3)=6$
B.函数 $y=f(x)-5$ 有三个零点
C.$g(x)=f(x)-x$ 是周期为 $4$ 的周期函数
D.线段 $y=x+\dfrac{16\sqrt 3}9,x\in[-2,10]$ 与 $y=f(x),x\in[-2,10]$ 的图象有 $6$ 个交点
答案 ABC.
解析 根据题意,有\[f(x)=\begin{cases} f(x+4)-4,&x<-2,\\ x^3-3x,&-2\leqslant x\leqslant 2,\\ f(x-4)+4,&x>2,\end{cases}\]如图.
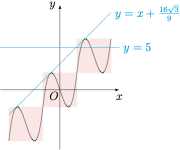
对于选项 $\boxed{A}$,$f(3)=f(-1)+4=6$,选项正确;
对于选项 $\boxed{B}$,$y=f(x)$ 与直线 $y=5$ 的公共点对应横坐标在区间 $[2,6]$ 上,有 $3$ 个,选项正确;
对于选项 $\boxed{C}$,由函数 $f(x)$ 为 $\mathbb R$ 上的奇函数且关于 $(2,2)$ 对称,可得 $g(x)=f(x)-x$ 关于 $(0,0),(2,0)$ 对称,是周期为 $4$ 的函数,选项正确;
对于选项 $\boxed{D}$,注意到\[(x^3-3x)-\left(x+\dfrac{16\sqrt 3}9\right)=\left(x+\dfrac{2}{\sqrt 3}\right)^2\left(x-\dfrac{4}{\sqrt 3}\right),\]于是直线 $l:y=x+\dfrac{16\sqrt 3}9$ 与函数 $f(x)$ 的图象在 $[-2,2),[2,6),[6,10]$ 上各有 $1$ 个切点,因此线段 $y=x+\dfrac{16\sqrt 3}9,x\in[-2,10]$ 与 $y=f(x),x\in[-2,10]$ 的图象有 $3$ 个交点,选项错误.
综上所述,正确的选项为 $\boxed{A}$ $\boxed{B}$ $\boxed{C}$.
