2025年11月浙江杭州市一模数学试卷 #18
已知 $F(1,0)$ 是椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的右焦点,过 $F$ 作直线 $l$ 交椭圆于 $A,B$ 两点,其中 $A$ 在 $x$ 轴上方.当 $AB\perp x$ 轴时,$|AB|=3$.
1、求椭圆 $C$ 的标准方程; 设 $P(4,0)$,
2、① 求证:$\angle APF=\angle BPF$;
② 设点 $M$ 在椭圆 $C$ 上,点 $N$ 是 $\triangle FMP$ 的外接圆与椭圆 $C$ 的另一个交点(异于 $M$),若 $MF$ 平分 $\angle AMB$,且 $\dfrac 1{|NA|}+\dfrac 1{|NB|}=\dfrac{\sqrt 3}{|NF|}$,求 $\cos\angle ANB$ 的值.
解析
1、当 $AB\perp x$ 轴时,$AB$ 为椭圆的通径,进而可得\[\begin{cases} a^2-b^2=1,\\ \dfrac{2b}{a^2}=3,\end{cases}\iff (a,b)=(2,\sqrt 3),\]于是椭圆 $C$ 的标准方程为 $\dfrac{x^2}4+\dfrac{y^2}3=1$.
2、① 设直线 $l$ 为 $x=my+1$ 且 $A(x_1,y_1)$,$B(x_2,y_2)$,根据题意,只需要证明直线 $AM$ 与直线 $BM$ 的斜率之和\[\dfrac{y_1}{x_1-2}+\dfrac{y_2}{x_2-2}=\dfrac{2my_1y_2-(y_1+y_2)}{(x_1-2)(x_2-2)}=0,\]联立直线 $l$ 与椭圆的方程,可得\[\left(\dfrac{m^2}2+1\right)y^2+my-\dfrac 12=0\implies 2my_1y_2-(y_1+y_2)=0,\]原命题得证.
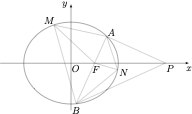
② 由 $MF$ 平分 $\angle AMB$ 以及 $PF$ 平分 $\angle APB$ 可得\[ \dfrac{|MA|}{|MB|}=\dfrac{|FA|}{|FB|}=\dfrac{|PA|}{|PB|},\]于是 $\triangle FMP$ 的外接圆上的点到 $A,B$ 的距离之比为定值 $\dfrac{|FA|}{|FB|}$,进而 $NF$ 平分 $\angle ANB$,设 $\angle ANF=\angle BNF=\theta$,则\[[\triangle ANF]+[\triangle BNF]=[\triangle ANB]\implies \dfrac 12\cdot |NA|\cdot |NF|\cdot \sin\theta+\dfrac 12\cdot |NB|\cdot |NF|\cdot\sin\theta=\dfrac 12\cdot |NA|\cdot |NB|\cdot \sin 2\theta,\]整理可得\[\dfrac{\sin\theta}{|NA|}+\dfrac{\sin\theta}{|NB|}=\dfrac{\sin2\theta}{|NF|}\implies \dfrac 1{|NA|}+\dfrac 1{|NB|}=\dfrac{2\cos\theta}{|NF|},\]因此 $\cos\theta=\dfrac{\sqrt 3}2$,进而所求 $\cos\angle ANB=\cos2\theta=\dfrac 12$.
