2025年高考全国I卷19题
设函数 $f(x)=5 \cos x-\cos (5 x)$．
1、求函数 $f(x)$ 在 $\left[0, \dfrac{\pi}{4}\right]$ 上的最大值；
2、给定 $\theta \in(0, \pi)$，$a$ 为给定实数，证明：存在 $y \in[a-\theta, a+\theta]$，使得 $\cos y \leqslant \cos \theta$；
3、若存在 $\varphi\in\mathbb R$，使得对任意 $x$，都有 $5\cos x-\cos(5x+\varphi)\leqslant b$，求 $b$ 的最小值．
解析
1、当 $x\in\left[0,\dfrac{\pi}4\right]$ 时，有 $\cos x\in\left[\dfrac{\sqrt 2}2,1\right]$，根据余弦的五倍角公式，可得\[\begin{split} f(x)&=20\cos^3x-16\cos^5x\\ &=4\cos^3x\cdot (5-4\cos^2x)\\ &=\dfrac{4}{\left(\frac 83\right)^{\frac32}}\cdot \sqrt{\frac 83\cos^2x\cdot \frac 83\cos^2x\cdot \frac 83\cos^2x\cdot (5-4\cos^2x)\cdot (5-4\cos^2x)}\\ &\leqslant\dfrac{4}{\left(\frac 83\right)^{\frac 32}}\cdot \sqrt{\left(\dfrac{10}{5}\right)^5}\\ &=3\sqrt 3,\end{split}\]等号当 $\dfrac 83\cos^2x=5-4\cos^2x$ 即 $x=\dfrac{\pi}6$ 时取得，因此所求最大值为 $3\sqrt 3$．
另法 函数 $f(x)$ 的导函数\[f'(x)=-5\sin x+5\sin(5x)=10\sin(2x)\cdot \cos(3x),\]于是\[\begin{array}{c|c|c|c|c|c}\hline x&0&&\frac{\pi}6&&\frac{\pi}4\\ \hline f(x)&4&\nearrow&3\sqrt 3&\searrow&3\sqrt 2\\ \hline\end{array}\]因此函数 $f(x)$ 在 $\left[0,\dfrac{\pi}4\right]$ 上的最大值为 $3\sqrt 2$．
2、即证明函数 $g(x)=\cos x$ 在 $x\in [a-\theta,a+\theta]$ 上的最小值不超过 $\cos\theta$．考虑到余弦函数的周期性和对称性，只需要证明 $a\in [0,\pi]$ 的情形．
情形一 $a+\theta\geqslant \pi$．此时\[a-\theta\leqslant\pi\leqslant a+\theta,\]于是 $g(x)$ 在 $x\in [a-\theta,a+\theta]$ 上的最小值为 $-1$，命题显然成立；
情形二 $a+\theta<\pi$．此时 $g(x)$ 在区间 $[a,a+\theta]$ 上单调递减，其最小值\[m\leqslant \cos(a+\theta)\leqslant \cos \theta,\]命题成立；
综上所述，原命题得证．
3、设函数 $h(x)=5\cos x-\cos(5x+\varphi)$ 的最大值为 $r(\varphi)$，则题意为求 $r(\varphi)$ 的最小值．根据周期性和对称性，只需要考虑 $\varphi\in[0,\pi]$ 的情形．注意到 $^{[1]}$\[r(\varphi)\geqslant h\left(\dfrac{\pi}6-\dfrac{\varphi}5\right)=5\cos\left(\dfrac{\pi}6-\dfrac{\varphi}5\right)+\dfrac{\sqrt 3}2\geqslant 3\sqrt 3,\]等号当 $\varphi=0$ $^{[2]}$ 时取得，因此 $b$ 的最小值为 $r(0)=3\sqrt 3$．
备注
$[1]$ 函数 $r(\varphi)$ 的解析式很复杂，因此考虑寻找它的一个下界函数 $p(\varphi)=h(x_0)$，通过 $p(\varphi)$ 的最小值 $p(\varphi_0)$ 来帮助求解其最小值，要注意取等条件是 $\varphi=\varphi_0$ 时，$h(x)$ 的最大值在 $x=x_0$ 取得．
$[2]$ 下界函数 $p(\varphi)=h\left(\dfrac{\pi}6-\dfrac{\varphi}5\right)$ 的意义是使 $y=\cos(5x+\varphi)$ 尽可能去削弱 $y=5\cos x$ 的波峰，而 $5x+\varphi=\dfrac{\pi}6$ 是第 $(1)$ 小题提示的预设波峰位置．
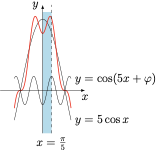
另法
考虑到余弦函数的周期性和对称性，只需要研究 $x,\varphi\in [0,\pi]$ 上的情形，下面证明 $b$ 的最小值为 $3\sqrt 3$． 设 $g(x)=5\cos x-\cos(5x+\varphi)$，则 $g(x)$ 的导函数\[g'(x)=-5\sin x+5\sin(5x+\varphi)=10\sin\left(2x+\dfrac{\varphi}2\right)\cos\left(3x+\dfrac{\varphi}2\right),\]在区间 $^{[1]}$ $x\in\left(0,\dfrac{\pi}4\right)$ 上，有 $\sin\left(2x+\dfrac{\varphi}2\right)>0$，而 $3x+\dfrac{\varphi}2$ 变化范围是 $\left(\dfrac{\varphi}2, \dfrac{3\pi}4+\dfrac{\varphi}2\right)$，进而 $g(x)$ 在 $3x+\dfrac{\varphi}2=\dfrac{\pi}2$ 时取得极大值，记该极大值点为 $x_0$，则\[5x_0+\varphi=2\left(3x_0+\dfrac{\pi}2\right)-x_0=\pi-x_0,\]其中 $x_0\in\left(0,\dfrac{\pi}6\right]$，进而极大值\[g(x_0)=5\cos x_0-\cos(5x_0+\varphi)=5\cos x_0-\cos(\pi-x_0)=6\cos x_0\geqslant 3\sqrt 3,\]因此 $b\geqslant 3\sqrt 3$．接下来证明 $b$ 取 $3\sqrt 3$ 符合题意． 取 $\varphi=0$，此时 $g(x)$ 在 $x\in\mathbb R$ 上的最大值即 $f(x)$ 在 $x\in [0,\pi]$ 上的最大值．根据第 $(1)$ 小题的结论当 $x\in\left[0,\dfrac{\pi}4\right]$ 时，$f(x)$ 的最大值为 $f\left(\dfrac{\pi}6\right)=3\sqrt 3$，而当 $x\in\left(\dfrac{\pi}4,\pi\right]$ 时，有\[\cos x<\dfrac{\sqrt 2}2\implies f(x)<5\cdot \dfrac{\sqrt 2}2-(-1)<3\sqrt 3,\]因此 $g(x)$ 的最大值为 $3\sqrt 3$，符合题意．
欢迎老师回归！！！