每日一题[127] 空间动态问题

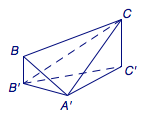
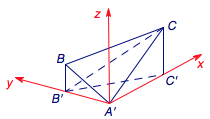
如图，已知边长为$1$正三角形$A'BC$的顶点$A'$在平面$\alpha$内，顶点$B$、$C$在平面$\alpha$外的同一侧，点$B'$、$C'$分别为$B$、$C$在平面$\alpha$内的投影，设$BB'\leqslant CC'$，直线$CB'$与平面$A'CC'$所成的角为$\varphi$．若三角形$A'B'C'$是以角$A'$为直角的直角三角形，则$\tan\varphi$的范围为________．

正确答案是$\left[\dfrac{\sqrt 2}2,\dfrac{\sqrt 3}2\right)$．

法一

如图建立空间直角坐标系，设$B(0,b,m)$，$C(c,0,n)$，则 $$\begin{cases}b^2+m^2=c^2+n^2=1,\\(0,b,m)\cdot (c,0,n) =\dfrac 12,\\0<m\leqslant n,\end{cases}$$ 可得$m$的范围是$\left(\dfrac{1}{2},\dfrac{\sqrt 2}2\right]$，而 $$\tan\varphi =b=\sqrt{1-m^2}$$ 的取值范围为$\left[\dfrac{\sqrt 2}2,\dfrac{\sqrt 3}2\right)$．

法二

注意到$\tan\varphi = \cos\angle BA'B'=\sin\angle BA'z$．考虑$\angle BA'z$为直线$BA'$与平面$ACC'$所成的角，显然其上确界（无法取得）为$60^\circ$，此时$\sin\angle BA'z=\dfrac{\sqrt 3}2$；其最小值当$BB'=CC'$时取得，为$45^\circ$．因此所求的范围为$\left[\dfrac{\sqrt 2}2,\dfrac{\sqrt 3}2\right)$．