该题改编于2010年北京中考第25题（压轴题）：
已知\(\triangle ABC\)中，\(\angle BAC=2\angle ACB\)，点\(D\)是\(\triangle ABC\)内的一点，且\(AD=CD\)，\(AB=DB\)．
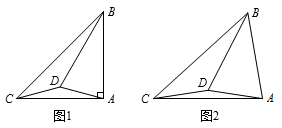
（1）如图1，当\(\angle BAC=90°\)时，求\(\angle DBC\)与\(\angle ABC\)度数的比值；
（2）如图2，当\(\triangle ABC\)为锐角三角形时，求\(\angle DBC\)与\(\angle ABC\)度数的比值．
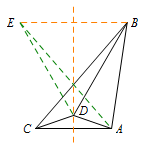
解 （1）此时\(\triangle ABC\)为等腰直角三角形，可以将其补成正方形\(ABEC\)，连接\(AE,DE\)．
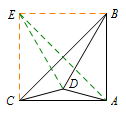由正方形的对称性可得\[\angle DEA=\angle DBC.\]由\(BA=BD=BE\)，得\(A,D,E\)三点在以\(B\)为圆心、\(AB\)为半径的圆上，所以\[\angle ABD=2\angle AED,\]故\[\angle DBC:\angle ABC=1:3.\]
（2）模仿（1）的解题思路，需要找到一个点\(E\)，使得\(A,D,E\)三点在以\(B\)为圆心、\(AB\)为半径的圆上，且\(\angle AED=\angle CBD\)，而这样点\(E\)是点\(B\)关于\(AC\)垂直平分线的对称点．
如图，作点\(B\)关于\(AC\)垂直平分线的对称点\(E\)，连接\(AE,BE,DE\)．
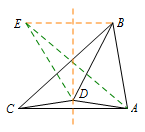由轴对称的性质可得\[\angle AED=\angle CBD,\angle BCA=\angle EAC.\]因为\(\angle BCA=\dfrac 12 \angle BAC\)，则\[\angle BAE=\angle EAC=\angle BEA,\]所以\[BE=BA=BD,\]即\( A,D,E\)三点在以\(B\)为圆心、\(AB\)为半径的圆上，故\[\angle DBC:\angle ABC=1:3.\]
练习 同上题条件，当\(\angle BAC>90^\circ\)时，请你画出图形，猜想\(\angle DBC\)与\(\angle ABC\)度数的比值并加以证明．
提示：