已知 $\triangle PAB,\triangle PCD$ 均为正三角形且 $PA=2PC$,则 $\dfrac{BD}{AC}$ 的取值范围是_____.
答案 $\left[\dfrac{\sqrt {21}-2\sqrt 3}{3},\dfrac{\sqrt {21}+2\sqrt 3}{3}\right]$.
解析 如图,有 $\measuredangle APB$ 与 $\measuredangle CPD$ 同向和反向两种情况.同向时 $\triangle PAC$ 与 $\triangle PBD$ 全等,此时 $\dfrac{BD}{AC}=1$.
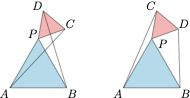
反向时,设 $\measuredangle APB,\measuredangle BPD,\measuredangle DPC,\measuredangle CPA$ 分别为 $\dfrac{\pi}3,\dfrac{2\pi}3+x,\dfrac{\pi}3,\dfrac{2\pi}3-x$,则根据余弦定理,有\[\dfrac{BD^2}{AC^2}=\dfrac{5-4\cos\left(\dfrac{2\pi}3+x\right)}{5-4\cos\left(\dfrac{2\pi}3-x\right)}=\dfrac{5+2\cos x+2\sqrt 3\sin x}{5+2\cos x-2\sqrt 3\sin x},\]设该代数式为 $t$,则\[2\sqrt 3(1+t)\sin x+2(1-t)\cos x=5(t-1),\]于是\[\left(2\sqrt 3(1+t)\right)^2+\left(2(1-t)\right)^2\geqslant \left(5(t-1)\right)^2\iff 3t^2-22t+3\leqslant 0,\]解得 $t$ 的取值范围是 $\left[\dfrac{11-4\sqrt 7}{3},\dfrac{11+4\sqrt 7}{3}\right]$,进而 $\dfrac{BD}{AC}$ 的取值范围是 $\left[\dfrac{\sqrt 7-2}{\sqrt 3},\dfrac{\sqrt 7+2}{\sqrt 3}\right]$,即 $\left[\dfrac{\sqrt {21}-2\sqrt 3}{3},\dfrac{\sqrt {21}+2\sqrt 3}{3}\right]$.
综上所述,所求取值范围是 $\left[\dfrac{\sqrt {21}-2\sqrt 3}{3},\dfrac{\sqrt {21}+2\sqrt 3}{3}\right]$.
