每日一题[4020]角参数解三角形

已知 $\triangle ABC$ 是锐角三角形，$CA>CB>AB=1$，且 $BC\cdot\sin B=2$，则 $\triangle ABC$ 的内接正方形的面积最大值为（       ）

A．$\dfrac 4 9$

B．$1$

C．$\dfrac 9{16}$

D．$4$

答案    A．

解析    根据题意，$\triangle ABC$ 的面积为 $1$，点 $C$ 到 $AB$ 的距离为 $2$，进而\[\dfrac{d(C,AB)}{\tan A}+\dfrac{d(C,AB)}{\tan B}=AB\iff \dfrac{1}{\tan A}+\dfrac{1}{\tan B}=\dfrac 12,\]其中 $\tan A$ 的取值范围是 $\left(2,+\infty\right)\setminus\{4\}$，内接正方形必然有一边落在三角形边上，分两种情况讨论，如图．设内接正方形 $DEFG$ 的边长为 $x$．

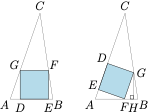
情形一     $DE$ 落在 $AB$ 上．此时\[AD+DE+EB=AB\implies \dfrac{GD}{\tan A}+DE+\dfrac{FE}{\tan B}=AB\implies x\left(\dfrac{1}{\tan A}+\dfrac{1}{\tan B}+1\right)=1\implies x=\dfrac 23,\]因此内接正方形面积为 $\dfrac 49$．

情形二     $DE$ 不落在 $AB$ 上．此时设 $G$ 在 $AB$ 上的投影为 $H$，则\[AF+FH+HB=AB\implies \dfrac{EF}{\sin A}+FG\cdot \cos\angle GFH+ \dfrac{GH}{\tan B}=AB,\]于是\[\dfrac{x}{\sin A}+x\cos A+x\sin A\cdot \left(\dfrac 12-\dfrac{1}{\tan A}\right)=1\iff x=\dfrac{1}{\frac{\sin A}2+\frac{1}{\sin A}},\]而 $\sin A$ 的取值范围是 $\left(\dfrac2{\sqrt 5},1\right)$，因此 $x$ 的取值范围是 $\left(\dfrac{2\sqrt 5}{7},\dfrac 23\right)$．

综上所述，所求内接正方形的面积最大值为 $\dfrac 49$．

备注    条件放宽到 $AB=1$，$BC\cdot \sin B=2$，结果相同．