每日一题[4015]相对运动与不动点

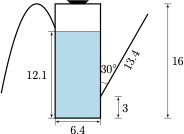
小申家里添置了一只新油壶，如图所示．该油壶的瓶身是一个底面直径为 $6.4~{\rm cm}$，高 $16~{\rm cm}$ 的圆柱体（不计厚度），瓶内装有 $12.1~{\rm cm}$ 高的油．其壶嘴长度为 $13.4~{\rm cm}$（不计体积），且壶嘴与瓶身的夹角为 $30^{\circ}$，壶嘴的底部距离底面的高度为 $3~{\rm cm}$．现将油壶从壶底一端缓慢倾斜，当油刚好从壶嘴流出时，油壶的最小倾斜角度为_______（精确到 $0.01^{\circ}$）．

答案    $14.2^\circ$．

解析    如图，油壶从壶底一端缓慢倾斜 $\theta$ 角，等价于液面 $GH$ 绕其中点 $I$ 旋转 $\theta$ 角，设旋转后的液面为 $G'H'$，则临界状态为直线 $G'H'$ 过壶嘴 $F$．

在 $\triangle G'EF$ 中应用正弦定理，有\[ \dfrac{|G'E|}{\sin\angle F}=\dfrac{|EF|}{\sin\angle EG'F}\implies \dfrac{12.1-3+\frac 12\cdot 6.4\cdot \tan\theta}{\sin(60^\circ-\theta)}=\dfrac{13.4}{\sin(90^\circ+\theta)},\]化简得\[\tan\theta=\dfrac{13.4\cdot \frac{\sqrt{3}}2-9.1}{9.9}\approx 0.2530,\]于是 $\theta$ 约为 $14.2^\circ$．