(2015年北京市海淀区高三期末理科)如图所示,在正方体\(ABCD-A_1B_1C_1D_1\)中,点\(E\)是边\(BC\)的中点.点\(P\)在直线\(BD_1\)(除\(B\)、\(D_1\)两点)上运动的过程中,平面\(DEP\)可能经过的该正方体的顶点是_______.(写出满足条件的所有顶点)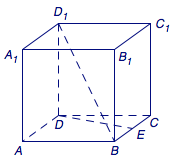
 正确的答案是\(A_1,B_1,D\).
正确的答案是\(A_1,B_1,D\).
当然,将正方体的顶点逐一代入验证是得到答案的简捷方法.但我们今天的问题是,确定平面\(DEP\)可能经过的该正方体表面的所有的点.
先将问题从正方体中抽离出来,也即三角形\(ABC\)中,\(AB\)为固定的线段,\(C\)在与直线\(AB\)异面的直线\(l\)上运动,那么三角形\(ABC\)所在平面扫过的空间区域是什么样子的?
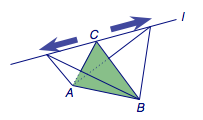 如图,不难想象,三角形\(ABC\)所在平面扫过的空间区域是过直线\(AB\)且与直线\(l\)平行的平面将空间划分成的两侧区域中的两侧.
如图,不难想象,三角形\(ABC\)所在平面扫过的空间区域是过直线\(AB\)且与直线\(l\)平行的平面将空间划分成的两侧区域中的两侧.
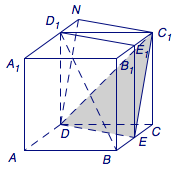 回到本问题,我们只需要过\(DE\)作平面\(\alpha\),那么正方体的表面上除去平面\(\alpha\),平面\(DED_1\)和平面\(DEB\)上的点即为所求的所有点,如图所示.
回到本问题,我们只需要过\(DE\)作平面\(\alpha\),那么正方体的表面上除去平面\(\alpha\),平面\(DED_1\)和平面\(DEB\)上的点即为所求的所有点,如图所示.

是不是有点儿问题,平面可以无限延展,举例说经过线段CC1中点和DE的平面就和直线BD1相交。
学习了!看透本质!